Recursive Learning Using Geogebra.

Last year was the first year I had my students making geogebra applets. Now that I look back, I think I went too fast at first, because their first function assignment was this. I think it was too much too soon. I may have frightened a few of them....so this year,

I'm slowing down now so I can speed up later.

This time around, they did that same linear function geogebra, but in several layers. I devoted a whole week to letting them get to know geogebra, using the linear function, with which they are already familiar from grade 10. I wanted to start with the linear so that this time around, they're learning about geogebra, as opposed to the math. Although frankly, the two never happen in isolation, but I digress. I had them watch my "Learning Geogebra" video, do the practices that went with them, and then create a new geogebra every day of the week, each one a copy of the previous with more information added to it. I gave feedback on every single version, and helped individuals so that everyone was good before going on to next version. Here's what we did:

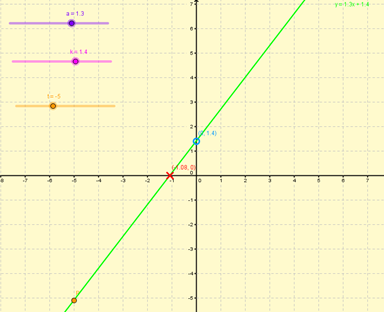
Day 1: Create a linear function controlled by sliders for slope and initial value & make sure the graph matches with your own knowledge of the linear function (ie increases for a > 0, flat for a = 0, etc)

Day 1: Sliders for a and k, rule y = ax + k

Day 2: Add a t-slider and a point P whose position is controlled by the slider, and which slides along the line, no matter how much a and k are. This was really hard for them, partly because they thought that sliders were only for parameters, which was my fault. Will have to do that better next year.

Day 2: t-slider and point P = (t, at + k)

Day 3: Add the initial value and the zero. Developed formula by: Got them to pick their own a and k, calculate I and Z, then use their own ggb to check. Survey everyone's calculations to get pattern, develop formula for I and Z, type in point to geogebra.

Day 3: I = (0, k) and Z = (-k/a, 0)

Day 4: special stuff, like conditional colours depending on whether the function increases or decreases (or is constant), displaying rule/coordinates using the "show value", or by using text boxes with objects in them.

Day 4: Cool fun pretty stuff

Bonus teachable moment

Some students didn't seem familiar with good computing practices such as saving subsequent versions with a new name, or file naming practices. The version created on day 1 was linear1, day 2 was linear2, etc. I discovered this when one student sighed and said it was tiring having to start all over each time....

And on that note, I made this for them:

And now, for the rest of this year, they're going to make geogebras AND USE THEM!!! To make more!!!!

I want them to do this for EVERY function we're studying. And not only make geogebras, but USE them. And not just because I tell them to, but because they are compelled to, in order to move their own learning forward, in whatever direction they choose. I'm seeing a cyclical formation, in which they use their own paper graphs, their own calculations, and their own instincts to create, use, then improve their geogebras, which then feed the next one...

The recursive learning: Create - Check - Use - Repeat

This week we're starting the absolute value function. Here's what I'm planning:

Tuesday: (Yesterday) Graph, on graph paper, many graphs of absolute value functions, and worked their way up until they could quickly graph and describe y = a |b(x - h)| + k. So now they knew what a graph should look like and why it looks that way.
Wednesday: (Today) Create version 1 with sliders for a, b, h, and k, and verify they're doing what they should by comparing to paper graphs. Also put in a vertex with (h, k) and make sure it's where it should be.

Thursday: Math lab! Use version 1 to explore relationships between parameters, to develop point P.
Friday: Create version 2 with time slider and point P, verify it using own calculations
Next week: To add initial value, domain, range, interval of increase etc

New Rule: Trust yourself first, geogebra second

What I really, really want to EMPHASIZE is that they verify, as much as possible, their own geogebra, using their own calculations, and not vice versa. Most importantly they verify NOT by showing it to ME and asking ME if it's right.

If this works, by the time they're done this, they will know the absolute value function like a boss!

And by the end of the year, they'll be total geogebrainiacs like me!

Audrey Learns to Code

I’m an online teacher for LearnQuebec, and I recently became a student in a classroom again, which hasn't happened in a long time. In my development as a teacher, I tend to spend a lot of time online, learning new things independently in a just-in-time fashion, but this post is about an instance in which that didn't work out, and I needed to be face-to-face with an instructor and peers. As usual, I learned way more than just what I set out to learn...

Audrey code

Until very recently, the only code I knew was Audrey code. For example, the first time I asked someone what “html” was, they answered me by saying “hyper text markup language.” I responded by blinking and saying thank you, which is Audrey code for “Now I have four more questions in addition to the one I just asked you.”

*blinks*

Probing further did not help. Every explanation seemed to make things worse, and intimidate me even more. Brow-furrowing, sighing, and wincing became part of my code. Nevertheless, I had a vague notion that it had something to do with the internet.

Coding? What is this coding?

Sometime later, I started seeing hashtags about coding on twitter, like #kidscancode, #codingforkids, and #coding. There was a lot of enthusiastic buzz from teachers about the many benefits of coding. Not only is it fun, addictive, & creative, but it improves understanding in math and languages as well. It was the creative part that interested me most!  I just wasn't sure of what type of coding everyone was talking about, or what exactly was being created. But I knew that before I tried to get my students to code, I needed to know how to do it myself - teaching usually works out better that way.

I decided to join codeacademy.org and try to learn coding on my own.  I started with JavaScript, because I had heard it referenced while using my favourite software, geogebra. The lessons were easy enough to follow, and I made “progress” according to the site, but I still felt like I was in the dark as far as what I was creating. Where would I use this JavaScript interactive thingy? I was missing the big picture, and I just couldn't keep at it without that. I felt constantly distracted, even agitated by that.

Google Apps scripts

Another effort that seemed, at the time, to be unrelated to html and coding was that I tried to learn how to write google apps script. I use google forms a lot, and there were specific things I wanted to be able to do with the data that my students were entering on those google forms. Off I went to google, and entered their google apps script “tutorials”. The problem here was that each link lead to so many other links that I lost my way very quickly. Unlike my codeacademy experience,  I was clear on what I wanted to create, but the tutorials didn't seem organized in a user-friendly way. In fact, one of the links lead back to codeacademy, specifically to their JavaScript course, which I’d already tried. What this had to do with google apps script I didn't know, which added to my confusion.

Convergence at Ladies Learning Code

These mysteries were finally solved for me on Sept 27 at a workshop in Ottawa called Ladies Learning Code. A friend had happened to mention to me that Sept 27 was National Ladies Learn to Code Day all across Canada. LLC (@llcodedotcom) is a not-for-profit Canadian organization devoted to teaching code to anyone who wants to learn in a comfortable, friendly, collaborative environment. They were having an introductory one-day workshop in many cities across Canada on Sept 27, so off I went to register. Unfortunately, the Montreal one was already full, so I decided to go to the one in Ottawa. I was persistent, because I was really interested in not only the coding, but the people who were organizing this amazing event, for free, on their weekend. People are endlessly fascinating to me, especially people who are passionate and creative.

I was not disappointed, in any way! Everyone working at the LLC session was a volunteer – our instructor, Jessica Eldredge (@jessabean),  the mentors (satellite teachers, one for every 4 participants), and the students from U of O. And everyone was friendly. You could tell right away that they were there to have fun and to help people. My favourite kind of people! I had a very strong sense that web developers are highly creative people who love doing what they do. And they love teaching other people how to do it! As for the participants, most were young, but there were a few my age, one of which sat at my table – coincidence? Probably not.

I'm sitting just right of centre. Coding!

At last - the Big Picture

Within the first few minutes of the session, a lot of my previous confusion was cleared up by our instructor, Jessica Eldredge. She said that html was what created webpages, and that you could think of webpages as being in three layers, each one in a different type of code:

1. The first is the content (text, pictures, links etc) which is created by the html.
2. The second is the CSS, which is another language altogether, and which makes the content have a certain colour or style or placement on the webpage. In other words, it makes it look pretty.
3. The third is the interactive elements, such as a gizmo on explorelearning.com. That’s where code like javascript comes in, and that’s where I had unwittingly started on my unsuccessful learning-to-code journey prior to this workshop. No wonder I had been confused – I had started with the last thing – javascript! Suddenly all the pieces fell into place for me. It felt like my mind was now truly open.

Workflow:

I really liked the way that the workshop was organized. It was kind of a mix of the flipped class and direct instruction. Jessica would spend a few minutes explaining something, then we would work for a while to complete the accompanying set of instructions, while getting lots of support from our “mentor.” Each group of four people had their own mentor. Ours was Gavin (@GavinNL), who was wonderful.  And he happens to be a math and science teacher! He was there in a heartbeat when we needed him, which was tremendously reassuring, but we also had the ability to move forward at our own pace as well, because we had already downloaded, prior to the workshop, all kinds of software and files, including all of Jessica’s slides and instructions. Hence the flipped element. I feel validated, because I use the flip in my own classes.

Audrey learned to code!

By lunchtime, I had made this:

Incredibly, I had written some html and css, and it had worked! We didn't get to the interactive stuff, but at least now I know what it is, what it's for, and where to go to continue to learn.

What else did I learn?

• Learning really is social. It means so much to be able to turn to someone, for a reaction, for help, for reassurance, and to offer it to them. Humans need humans.
• I like having the option to move ahead or go back as I wish. And at different times during the day, I did both. Although at around 2:30, my saturated mind ground to a complete halt.
• That option to move at one's own pace is only truly available if the material given is well organized, easy to find, and contains good visuals and examples, which Jessica's did.
• Hearing someone say something is way more powerful than reading it to yourself.
• A webpage is a file! That blew my mind. To see my webpage, I double-clicked on a file with .html at the end. I don't know why that was so eye-opening for me, maybe because it made it all seem a lot less like magic and more like logic.
• I need to have the big picture to learn some things. Otherwise, I'm constantly distracted and agitated.
• Web developers are highly creative people who are passionate and love to teach other people how to do the same! I'm encouraging my own kids to learn, because they are very creative people too. So far no luck, after all, I'm their mom.
• Finally, there are an awful lot of people out there who love to teach, and are really good at it, but very few of them do it for a living like I do. I'm lucky like that.

What's next?

So what am I going to do with this? Not sure yet - I had a vague notion that I would rebuild my own blog from scratch, but that seems like it might be a bit too much to start off with. I remember feeling this way when I started to learn geogebra  - I had no idea what to make with it, I just knew that it was really really cool. That's where I am now - any suggestions would be more than welcome! And that's not Audrey code for anything!

I'll Take a Linear Combo To Go

This went well.

It was one of those classes when I felt like I learned at least as much as they did, and all kinds of unexpected things happened. During class and as I wrote this post.

The idea that I wanted to get across, with as few words as possible: That under certain conditions, for every answer, not only is there is always a question to go with it, but there is only and exactly one question that goes with it.

The exact mathematical version of that, if you're into that: Given a resultant vector, and two other non-collinear vectors, under certain conditions:

1. There is always a way to linearly combine the two to get the resultant.
2. There is only one way to linearly combine  the 2 that will work out to that resultant.

This is what we did in class, on the whiteboard, which, remember, is all online, so everybody can write on and see the same board at the same time, and talk to each other while they do.

First I showed them this:

and said: "The red vector is the resultant of some number of blues and some number of greens being added. Since the red vector is the answer, what am I going to ask you to figure out?"

Someone said "The question?" Bingo. In other words, they had to figure out how many blues and greens add up to the red.

I then put them into their breakout rooms (the online equivalent to groups at tables) where they moved the blues and greens around to see how many of each would add up to the red.

Here are a couple of their results:

Everybody got that 6 blues and 4 greens were needed, which was what I expected. I wrote "6 blue + 4 green = red", and talked about how everyone got the same solution...

Audrey's first light bulb moment:

"But," said one student, "we didn't all get the same solution." She explained that really these two solutions weren't equivalent, because the paths from start to finish weren't the same. Light bulb - we're not talking the same language! I'm talking numbers & algebra, and they're talking pictures. It was a great opportunity to clarify exactly what I meant by "solution" right at the start. I meant the total number of blues and the total number of greens, not so much the sequence/path.

So I asked if they thought that there was some other NUMBER of blues and greens that would work, not just a different path but a different numerical combo. I expected and hoped they'd come back with, "Why no Mrs, there isn't any other combo." Back they went. Here was a most interesting result, which lead to

Audrey's second light bulb moment:

...in which there are more than 4 greens and 6 blues, right? TOTALLY awesome. First we traced a path that actually lead to the resultant. Now I got to connect the idea of opposite vectors to subtracting - and establish the convention that if you go one green forward then one back, you've really cancelled out one green with another. Saw a lot of "OOOHHHHH!!!" light bulbs going on everywhere today. We finally agreed that 6 blue and 4 green is the only and simplest numerical solution. Non-verbal idea 2 done!

Now that I'm blogging I can see:

I just loved how all these things came up so naturally and as a result of THEIR manipulations and thoughts - perfectly legitimate and logical thoughts, too. I would never have thought of bringing up any of these issues, which means I would have missed out on making clear the ideas that absolutely needed to be clear before we could move on. Together.

But move on we did. Time for me to mess them up again.

I kept the red, but changed the blues and the greens like so:

Now they're trying to get the exact same answer, but find a different question to go with it - were we only able to get the red the first time using those particular blues and greens that I had lovingly hand picked?

This time, I was not looking for WHAT is the question for this answer so much as IS there a question for it at all. Very quickly I had groups asking if they could change the direction of the blues or greens.

Me: *bats eyes* Well if you insist, I suppose you can make them into their opposites, but that's it.

In fact, it was only possible if the blues got opposite-ed AND you could use part of a blue or green. In fact, the previous discussion on opposites fed into this one very nicely. This lead very naturally into the motivation and meaning for non-whole scalars and negative scalars:

I casually slipped into the notation used for linear combinations, as you can see.

Now that I'm blogging I can see also:

The ease with which they could move the arrows, flip them so they were opposite-ed, and cut them into pieces cranked up the potential a few notches. If I had had them drawing, erasing, etc it would have taken way too long and been way too frustrating, not to mention the colours wouldn't have played a part. It was so much easier to say red, blue, green. Plus it's more fun for them to be manipulating things, and this is as close to observable & active learning as I can get online. Mind you, if I had had any colour-blind students, that would have been a problem.

Back to non-verbal idea 1:

Me: But is it always possible, no matter what blue and green we start with?

Some of them: Yes.

Some of them: No.

I let one group make up their own blues and greens, copy them, and voila, it was still possible. This would be the equivalent of a magician saying pick a card, any card. Now we've established that no matter what the blue and green, we can always get the red using a linear combo of them. Non-verbal idea 1 done.

Under what conditions?

OR CAN WE?!?!? Time to motivate the "under certain conditions" part. For the next part we were all together, no more break out rooms:

I asked how many "a" vectors I would need to make the "c" vector:

Astounding and wonderful to find another hole in their comprehension! Some said 4, or -4, or "You haven't taught us how to multiply and change the direction of the vector." We did some trials together, lining up 4 of them, lining up -4 of them, and eventually agreed that there was no scalar multiple of "a" that would result in "c". Even though they "knew" that collinear vectors are scalar multiples of each other, that's not the same kind of knowing as knowing that non-collinear vectors are NOT scalar multiples of each other, and never will be. I just read that back to myself. Sorry for all the negatives.

Now that I'm blogging...you get the idea:

At this point, I just felt like this lesson/activity/whatever you want to call it, was going really well. So many ideas, so many levels, so much participation, so little time! AND I had at this point stopped using colour-talk, and very sneakily slipped into the proper vocabulary: resultant, collinear, scalar multiple, linear combination. SO I was doing more talking here but I was using official language. This might have been a good time to put in a hinge question, to check that they were all still with me.... next time.

"But," I said, "what if I told you you could use vector a AND some other vector, like this?"

They got this easily, based on the manipulations they'd just done - yes it's possible. But this was another layer of knowing - we'd already established that it's always possible but now they saw that it's actually impossible without the other vector, in order to swing things back to the resultant.

Me: Will it always be possible to get c as the resultant, as long as I have two other vectors to combine linearly?

Them: Yes, Mrs, geez, we get it already.

Me: Really? You sure?

Them: *blink collectively*

Me: *smiles evilly*

Me: What if the other vector was this:

Boom! More OHHHHHH's.  Just established what those"certain conditions" are. The two have to be non-collinear, or else you can't swing back toward the resultant.

And the linear combo to go:

If I had had just a little more time in class, I would have moved into this next, but I didn't have time so I assigned a few of this type of question:

What linear combination of  <-2, 7> and  <1, 4> results in  <-1, 26> ?

Next day, the colours paid off:

Many had difficulty, not all, but many. I saw my job as helping them see the question first. Showing how this question was the same as the blue, green, and red arrow questions. In fact, it was really handy to be able to refer to the colours and make this abstract question more concrete that way:

n<-2, 7>  +  m<1, 4>  =  <-1, 26>

One student said he had tried solving these by trial and error, which at first was easy, but got harder as the examples got harder. He asked if there was a better way. Once he saw that it was a system of linear equations, he and others again went "OOHHHH!" It was an aha moment that algebra really is useful sometimes.

Now to figure out how to do this if I have a colour blind person in my class.

A Math Teacher Teaching Science?!?

Last year I started to wonder what it would be like to teach a new course, because I've taught the same courses for a while now. I guess I made the fates laugh heartily, because guess what happened?!?

This year I'm teaching grade 10 science for the first time. I had taught science and physics in the very distant past, but I am a math teacher by trade and by comfort. New course? Check.

But the science isn't the only new thing. The students in my class happen to be teen moms, who are in a program and a school designed for their particular situation. Which means that they aren't able to do much, if any, homework between classes. So no flipped-class videos either! Whatever happens, has to happen during class. New student situation? Check. New strategy? Check.

AND there is a provincial exam at the end of the year, which they have to pass in order to graduate from high school. Just so long as there isn't too much pressure!

Week one: In which I go to an actual school

Last week was my first week with the girls, and since their school isn't far from here, I drove downtown to meet them face-to-face. (If you're wondering why a teacher would even mention this, just know that I teach online, and don't usually get to meet my students.) We had a friendly chat, and I got to meet their babies, because the nursery is right there in the school. Which one girl said made it hard sometimes, because when you hear your baby cry and you can't go to them, it hurts. I certainly get that.

It was especially important for me to meet these students right away, because if anything is going to get them through this year, it'll be relationships. Sometimes when you're tired and fed up, the only thing that makes you show up is that you like the person or people you're going to see. I hope that's how they'll feel.

Week two: Atoms & baby germs

This week so far has been good in the sense that I've gotten a lot done during class - so far, we've done the different models of the atom, electron configuration, and the periodic table. But there have been a lot of absences already - you know how it is when you're exposed to baby germs, the strongest germs known to man or woman. I really have no idea how to deal with that.

Behold all the science things!

For the last two weeks, it's been Christmas for me. I got to open the Science folder in Smart Notebook's Gallery - woo hoo there's gold in there! And now all those gorgeous geogebras that people made for science? They're mine to covet! That part's been fun - I always felt like science people just had more stuff!

An Act of Love

The greatest impact of all is that I met with the ladies who run this program. They are so passionate, devoted, no-nonsense, and team-oriented that I feel like I've been hit with a lucky stick just to work with them. I've met only a few people in my life that I could honestly say this about, but what these ladies do every day is an act of love. It's hard work, it doesn't pay a lot, it's not glamorous, and sometimes the people you're trying to help only get that long after they've exited the building. But they do it because they love it and they know it's important and they own the job.

Kind of like what moms do for their kids.

Less Paper, Not Paperless

This past week's #flipclass chat exit ticket was to write a post about our workflow, which I have to admit I didn't even know where to start with. Then Brad Holderbaum helped me out by asking me this:

@a_mcsquared Can you reply more on the paperless classroom how you do it
— Brad Holderbaum (@HolderbaumBrad) August 12, 2014

This is in response to my answer for Q2, which was about how paperless our classroom is. Now that I am actually thinking about it, I'm not sure mine's as paperless as I thought. Since I teach online, everything that flies between me and my students has to be, at some point, in digital form, but as it turns out, there are wildly varying degrees of paperless-ness during the year. To measure the degree, I'm looking at how much paper is involved in each task at each of these stages:

1. The actual task
2. How I deliver that to them
3. What they do
4. How they deliver that to me
5. How I assess
6. How I deliver that to them

I looked at five different types of tasks, and filled out this table with green = no paper, red = paper. It made it easy for me to see that the most recent things I've been giving them are, or can be at least, 100% paperless.

A little more detail about those tasks:

Tests:

When I give a test, I email it to each of the schools' secretaries, who then prints them up. The students then write on it, and it then gets either scanned or faxed to me. If it's faxed, obviously, there's more paper used. Either way, from then on, it's paperless. I don't put my corrections on any paper. By now their tests are all in digital form, either as an image or a pdf, so I send them to Smart Notebook, where I can mark them up with digital ink, stickers, whatever. Here's how that actually looks in real life:



Assignments: 

These might be a worksheet, or a set of problems, or one big multi-step problem (called a situational problem here in Quebec). I deliver it via our CMS (Sakai) but I know most of the students print it up right away. I always give the option to do it on paper, but unlike the tests, they can also do it using some digital tool, such as voicethread, or geogebra, or whatever they choose. I usually offer bonus points for that - questionable I suppose, to motivate using marks, but hey. At any rate, as long as it's presented so that I can follow their reasoning, it's all good. If they go with the paper, then it's exactly the same degree of paperlessness as the test, but if they do it digitally, for example, like this, I create a rubric in Smart Notebook, fill it in with digital ink as I do the tests, export to pdf, then upload that to their dropbox on Sakai. Here's what that looks like to the student:

Blogpost / Geogebra / Portfolio entries:

My students all have their own blogs, as well as digital portfolios. The blogs are of course viewable by anyone, and they are linked from the classblog, but the portfolios are only viewable in our immediate community. Usually the post or the portfolio entry is about an applet they're creating using Geogebra, my favourite dynamic geometry software. Regardless of which of these three they're doing, the degree of paperlessness is the same - 100%!

Toward the end of last year, I gave them a task involving all three of these things. I wanted them to use their portfolios to track their own progress and to get feedback from me, then use geogebra to confirm and organize their learning, and once they were ready to commit, share it with the world on their blogs.

Here's how that looked: assignment description, assessment description, student's post, and a filled-in rubric:

Note that all of these points came directly from the assessment description that I linked above. I didn't want my students to be surprised at how I would be assessing their work! Next year, I plan to get them involved in creating the rubric itself.

I can't show any students' actual portfolios of course, but I did do a post that showed snippets from their reflections for another assignment, this one involving just creating a geogebra. (I got their permission to share, and they're anonymous anyway.) You can read about that here if you're interested to know what I mean by portfolio entries.

Good on paper:

Full disclosure - several times a week, my students write notes, on paper, based on the voicethreads that I create for them to watch. If I put that into the table above, IT WOULD LOOK LIKE THIS. I know it's a lot of paper, but I also find that writing on paper can be a worthwhile thing to do, so I don't know if I'll ever want to change that. I'll reduce, but I don't see myself ever being 100% paper-free. Besides, like my mother, I love books too much!

After the Ten Stages of Twitter

This post has been in draft mode for about 3 months. I've never stared at that publish button for as long as I have for this one. Then this summer, at Twitter Math Camp, in Jenks, Oklahoma, this happened:

Photo credit: Greg Taylor @mathtans

What is this? This is one of the slides presented by none other than Dan Meyer. His presentation was about who the Math-Twitter-Blogosphere (#MTBoS) is and, among other things, how the members of it use twitter. He showed us some very interesting stats, some of which are in this picture. Under #FOLLOWING are the top three people in the MTBoS in terms of how many people they follow. If you look closely, you'll see my twitter handle. Yup. If Greg had taken a picture of me at this moment it would have looked like this:

♫ Psycho shower scene music ♪

Because it means out of all the people in the MTBoS, almost nobody follows as many people as I do. Dan mentioned that he'd like to hear about how one would manage this many followees. Well, here it is. How do I manage it? I don't. Which is why I was writing this for so long. Nothing like being a statistic in a Dan Meyer presentation to motivate finishing that 3-month-old blogpost! Here it is, folks:

I remember when I read The Ten Stages of Twitter, by Daniel Edwards. I recognized every single one of those. But now I'd like to add a few more stages to his list, based on my own recent experience, maybe yours too.

Stage 11: Vexation.

I'm not really sure when this stage started, all I know is that at some point, my twitter experience started to sour, and to distract me from my growth as a teacher. Reading my twitter feed used to make me feel stimulated and inspired, but suddenly, I was getting vexed instead.

Part of the vexation was sheer quantity. I was following too many people. Checking the general feed felt like drowning, getting pulled in too many different ways. I had tried to filter by creating all kinds of lists, but they also got too big. My "top ten" list had 27 people on it. And I wasn't very good at remembering to check each list anyway.How did I even end up following so many people? Some people I followed simply because they were nice enough to follow me, and after all, I am Canadian. But whether or not I ever saw any of their tweets afterward, or connected at all...for the most part, no. I couldn't honestly call twitter my PLN, because everyone can't be in your PLN. If yours includes everyone, then it really includes no one.

But that wasn't the main reason for the vexation.

Some tweets were actually upsetting me.

I'd see an unbelievably sarcastic, condescending tweet about someone or something, and wonder how an educator could behave that way - especially toward another educator. I often thought - How would this teacher feel if they suddenly realized that their students had witnessed this whole exchange? Would they be proud of themselves? Would they feel they had modeled respectful debate? I know no one's perfect, but shouldn't we try to move through this world the same way we want our students to? That means we treat each other the way we want to be treated, even on twitter.

I have to admit, some of the aforementioned tweets were also very funny, but does that make it okay? I don't think so, but based on how many retweets these funny retorts got, it seemed that on Twitter, as on the playground, sometimes mean was masquerading as clever.

And then there was the twunning.

In real life, when you speak directly to someone, and they don't answer you, it's rude. If they then turn to answer someone else instead, it's downright insulting. And if that happens over a sustained period of time, it's a form of harassment called shunning. I don't know what it's called on twitter, twunning maybe? But it sucks.

I wondered if it was just me - maybe I'm not supposed to have the nerve to be addressing a tweet to someone who has thousands of followers. And of course I get that some people don't have enough time to answer all the tweets they receive. But then someone like Darren Kuropatwa or Pernille Ripp would have that excuse, right? But they DO answer. And besides, isn't that what twitter is for? The chance to connect with ANYONE?

Stage 12: Self-analysis

Instead of getting more and more upset, I had to ask myself what I really wanted out of twitter. Because clearly, either I was looking for the wrong thing, or looking in the wrong place.

I realized that to a certain extent, I was looking for attention. I saw my melancholy self sitting by a stream with a dozen fishing lines going, resting my chin in my hand, just waiting for a bite. Not appealing. So I had to face up to that childish need. This was really hard to admit. *pats self on back*

But I was also looking for authentic and meaningful interaction - with people who are interesting and interested in the same things I am, who challenge me, or who just make me smile. But interaction is by definition two-way, not one-way. So people who tweet some deep thought, then get a zillion responses but never engage beyond that, (or only do so with a select few), have at it, but that's not what I was looking for at all. At all.

Most important of all though -  I needed to take care of the solid connections I had made already. I knew that the twitter fire hose was making me miss out on the good stuff - not only the info that I could truly use, but tweets from people who really mattered to me, with whom I did interact. Those people need interaction and responses too, just like me.

Stage 13: Re-twittering

It was about destroying in order to rebuild:

First of all, I got rid of a lot of the lists that I had.

Then I unfollowed a lot of people. Unfollowing someone is hard, because I'd never want to hurt someone's feelings. I didn't do it to be mean though, or as a tit-for-tat thing, I just felt I had to trim it down. It's simple logic to me - if interaction is what I want, and it's not what's been happening with @PersonX, I unfollowed. But that started to be really tedious and it felt really negative too.

So I took another tack - a more positive one. I decided to take some responsibility toward my actual, real, honest-to-goodness PLN. I realized that a PLN isn't just about what you get, it's about what you give.

I made a new list. A really short one. These are people who already consistently interacted with me. Some on a daily basis, some less frequently, but at least consistently. Or who did any of the following:

• get me
• are nice
• answer me
• have some common interests to mine, but that's not an absolute necessity

This list has become my PLN. There are teachers on it, there are gardeners on it, there are relatives on it...I can't even characterize any commonalities other than that I know I'll get just as much as I give to these people. I'm sure that being on this list confers no special honour, because it's only a confirmation of a relationship that already existed anyway. By the same token, I'm sure that not being on it won't upset or insult anyone. I don't assign such importance to myself. But I do to my feelings, and to my PLN.

My New Twitter Routine

Now the first thing I do when I get onto twitter is check my daily list. It currently has 46 members. Totally manageable. It doesn't take long for me to scroll through that feed, I see everything these blessed people are saying, I respond because I want to and I can! I feel like I'm in the company of old friends.

One last stage: when online becomes face-to-face:

I hope everyone gets to this stage eventually. When you get to meet these people face to face, after being twitter friends for years. I had the opportunity to do that at a tweet-up in Ottawa, then at Flipcon14, in Mars, Pennsylvania, and also at Twitter Math Camp, in Jenks, Oklahoma. This is a whole other-nother level. (apologies to English teachers everywhere.) Now when I read the tweets of these people, I hear their voices, I see their smiles, I remember moments we shared. The line between online and f2f just got blurred.


Twitter, like life, is a double-edged sword. There's just as much potential for good experiences as for bad ones. But I do have way more control over my twitter experience than my life one, and this change of tack has made a HUGE difference. No more vexation, WAY more growth, and wonderful friendships. I just hope my Daily list doesn't get out of control.......cue Psycho shower scene music again......

Big Ideas at Flipcon14

Flipcon14 took place in Mars, Pennsylvania June 23-25, and I'm happy to say I was there. I had previously attended Flipcon12 in Chicago. My perception may be a little skewed, but it felt like this conference had a Big Idea feel to it that I don't remember from the Chicago one, maybe because I was still a relative beginner then. Where did this feeling come from?

First from the keynote speaker, Molly Schroeder. She said these three words:

Think - Make - Improve.

That's what all these teachers have been doing with their own work, with other teachers' work, and it's what we want our kids to do.

Later, Brian Gervase said this, which I just had to tweet:

The flipped conferences have gone from being about technology to being about pedagogy @bdgervase #flipcon14
— Audrey McLaren (@a_mcsquared) June 25, 2014

Throughout the conference, I found that even though most of the sessions I attended were not specific to math, what I heard was nevertheless applicable to any subject. Big concrete ideas that are making their way through the Think - Make - Improve cycle, taking on new colours as they move into different subject areas, then branching out further, in a sort of learning fractal.

A rundown of what went down, and my takeaways:

Day 1: Session A: Andrew Thomasson & Cheryl Morris:

Creativity: Biggest takeaway for me was that routine is a significant factor to creativity. Counter intuitive for me! I always thought it happens when it happens, you can't schedule it. Blogging, for example - whenever I've heard people say they stick to a blogging schedule, I've thought, well not me, I wait to be inspired. But it turns out there is evidence that routine really does help people be more creative.

Gradual release of responsibility: The year begins with bootcamp, and ends with work for which the student assumes full responsibility. During bootcamp, the essential skills are covered, like how to watch a video, how to talk to peers, how to take notes. For math class, it will be about those exact same things, plus using Geogebra and Desmos. 

Opportunities to practice: no grades for these, simply practice on the essential skills but building in variety, such as taking notes from a variety of media, video, text, or a website. Perfect for what I'm planning for next year - giving my students more geogebra and less direct instruction, so they'll need to take notes from their own explorations with geogebra.

Grammarly: Cheryl showed how she uses this tool with her students. She feeds the students' text to grammarly, which it then scans it for grammatical or spelling errors, then it reports how many errors there are. It's up to the kids to find them and fix them! I'm going to do the same with math examples, maybe even create a geogebra with mistakes in it, and have them find and fix them. I can train them to use geogebra at the same time, kill two birds with one stone if you will.

Networking by subject
This was a great idea - one entire slot of time devoted to informal chatting amongst people who teach the same subject. Of course, I headed to one of the math rooms. We organized ourselves into groups by level, and I ended up in a circle of about 10 people who teach senior high. We had a great time just sharing our questions, ideas, general thoughts. There was a teacher there who had come all the way from China (if I recall correctly)!

This was just the right amount of subject-specific stuff for me. And even this discussion yielded some generalizations - via Steve Kelly, for example, about how kids organize themselves into groups according to their ability, which usually turns out to be about 4 different levels.

Soon after this, I started to feel overwhelmed, even though it was still day 1. I expressed this to Steve Kelly, who was kind enough to tweet it out:

@a_mcsquared "I need a break from hearing awesome things" #Flipcon14
— Steve Kelly (@bigkxcountry) June 24, 2014

Session B: Book panel:
Next it was time for all the coauthors of this wonderful book:

to join Jason Bretzmann, our publisher and tireless supporter, for the panel discussion he organized. Jason gave a wonderful presentation about the book, and had some questions for us all to take turns answering. It was an honour to be included in this group of talented people.

Does it kind of look like Jason has a halo? Just saying.

That evening we were all bused to the beautiful Carnegie Science Center in downtown Pittsburgh. I have to say, I had no idea that Pittsburgh was such a beautiful city! Our view from the science centre cafeteria was stunning - we were sitting in a valley, where two rivers become one, surrounded by an astonishing amount of greenery. Lots of huge yellow bridges, too! We had a great time eating, learning, and DANCING. Michelle Karpovich said it best:

#flipcon14 attendees have gone wild, dancing on the second floor! In this digital age, #whathapoensatflipcondoesntstayatflipcon!
— Michelle Karpovich (@mkarpovich) June 25, 2014

Day 2: Session C: Jonathan Thomas-Palmer
Videos: Jonathan makes physics videos full-time, so he's pretty good at it. He used to teach, and flip his class using videos, but found too many students did not watch them, so decided to make them so good that they would WANT to watch them. He gave us tips on making engaging videos.

Audio is of prime importance, get a really good mic, check your audio level, don't film outside
Talking head should be doing more than just talking - pick up stuff, point to parts of presentation, anything to vary. Don't film with light behind you.
Frequent visual changes ie text popping up that paraphrases what speaker has just said, arrows, callouts

Jon cautioned against trying to make something like this, with one person playing multiple characters:



....unless you have a professional grade software. Darn. That looks really fun.

Session D: Brian Gervase
This was one of those sessions that got me so worked up that I didn't take any notes. I spent this session either tweeting what I was hearing Brian say or just picking my jaw up from the floor, being stunned that someone else could speak my thoughts so eloquently and passionately. Brian's session was called Flipped Assessments. He uses mastery with his classes. Here are some of the tweets I managed to make, apart from the one at the top of this post:

These LMS 's are the teaching assistant you never had @bdgervase #flipcon14
— Audrey McLaren (@a_mcsquared) June 25, 2014

Problem we all have is trying to cram old curriculum into new pedagogy @bdgervase #flipcon14
— Audrey McLaren (@a_mcsquared) June 25, 2014

@bdgervase "I'm a 24/7 teacher now." Me too. I'm ok with that too. #flipcon14
— Audrey McLaren (@a_mcsquared) June 25, 2014

Anyone who knows me at all knows what my favourite math edtech tool is, and at one point during the session I became afraid I might lose what little professional composure I still had:

Math Portfolios!!!! OMG!!! If @bdgervase starts talking about @geogebra I'm gonna lose it I swear #flipcon14
— Audrey McLaren (@a_mcsquared) June 25, 2014

As it turned out, Brian ran out of time in his session, which is probably for the best, because he later replied:

@a_mcsquared @geogebra if I had ten more minutes you would get your geogebra!
— Brian Gervase (@bdgervase) June 25, 2014

Session E: Crystal Kirch
Crystal explained her WSQ system, which she uses in her math class.  I had read about it, and had even tried a form of it before, but it's always way better to hear things explained f2f and see it for yourself. Crystal's talk, like all of her writing, isn't just about the details of what and how she does the WSQ, or the TWIRL, it's much deeper and further-reaching. Brian said it best:

@crystalkirch has a ton of acronyms, but they're rooted in sound pedagogy and education theory. #flipcon14
— Brian E. Bennett (@bennettscience) June 25, 2014

Crystal also spoke of routine in her class, just as Andrew and Cheryl did. Bigger ideas included Organization, Accountability, Processing, Feedback, and Discussion, all features of her classroom, which we can all use, regardless of what we teach.

Session F: Stacy Lovdahl and Eric Marcos
Stacy gets her students to create videos as projects, and Eric's students create videos to help their peers' understanding. In either case, the underlying idea is purpose. Kids learn best when they're making something that they see the purpose of. Think - Make- Improve must be happening constantly when kids make videos. There are other benefits, though, such as kid-friendly language, both in the video and in the feedback other kids can then give:

Kid vids + kid feedback like a digital jigsaw @braveneutrino #flipcon14
— Audrey McLaren (@a_mcsquared) June 25, 2014

One example of the benefits of student-created videos was Stacy's - you get 16 kids to each create a video showing an example of a chemical change, and boom, not only did they engage in their learning, have a purpose, but they also now have 16 examples! My favourite rationale for kids to present their learning this way instead of in front of the class is here:

When a kid does a presentation in class the other kids are just there to make them nervous @braveneutrino #flipcon14
— Audrey McLaren (@a_mcsquared) June 25, 2014

Biggest takeaway, biggest idea from Flipcon14:

There is so much variety in what teachers who "flip" are doing, that the word really doesn't mean anything anymore. But I will still use it because:

#flipclass has come to simply be the name of a community to which I belong. It's no longer about what or how, it's about who.
— Audrey McLaren (@a_mcsquared) June 28, 2014

There's knowing and then there's KNOWing

Knowing:

My students did this activity yesterday, in which they unwittingly drew a parabola using geometry instead of algebra. So they "knew" about the focus and directrix of a parabola, and that all the points on a parabola are the same distance from the focus as they are from the directrix. And they "knew" the formula c = 1/(4a).

But I had a sneaking feeling they didn't really KNOW, you know?

KNowing:

So today I showed them this:

...and asked "Which point is the focus of this parabola?" There were guesses for each of the colours. Some said they all could be the focus. Bingo. They know what it is but not what it isn't. That's not KNOWing.

"If the pink one is the focus, then which line has to be the directrix?"

Everyone went with the pink line of course, but their reasons were varied:  because the colour matches, because it's the farthest away, because it's the same distance from the vertex as the pink dot.

Right. We've just established that as soon as you have a focus, you also have a directrix - they work as a team. That's a slightly bigger picture. Also I need to knock it off with the colour coding.

KNOwing: 

"Is it possible that any one of these could be the focus, as long as we pair it with the correct directrix?" Some said yes, some said no. 

Time to test out their hypotheses. I had everyone make a dot somewhere on the parabola with their initials.

"Draw L1 and L2 for your point using the green focus/directrix."

The board looked something like this:

It was very fortunate that K picked the vertex for her point!

"Does anyone's point have L1 = L2?"

K's did, no one else's though. 

"Well does that mean the green point is the focus or isn't the focus?"

Great discussion on why it isn't - it's not good enough to have one point on the parabola with L1 = L2, they ALL have to have it. They knew that yesterday, but this was knowing on a different level. I think the fact that each person "owned" a different point reinforces the all or nothing idea here.

Then each person picked a new points, and we tested out the blue pair. As soon as ONE person's point didn't work, the reaction was immediate - it can't be the right pair. 

Now they knew that there is only ONE possible location for the focus and directrix of a parabola. Move anything and it doesn't have the L1 = L2 property.

KNOWing:

We finally tested the pink pair and found it to be the actual focus and directrix. Now they knew where it was and where it wasn't, and there's only one possibility for the former.

Way to drop the ball McSquared:

The final point I wanted to make was the connection between what they just did and the formula c = 1/4a. Not the algebraic connection, but the bigger, deeper one:

The numbers are connected like this: Change the value of a, and you'll change the value of c, and vice versa.

The things are connected like this: Change the parabola, and you change the focus and vice versa.

Unfortunately, that part was just me talking, which I'll replace next time with them doing something, not sure what. Something involving matching parabolas with c values and focus/directrix pairs.....it was time to zoom out here and I dropped the ball, but I'll pick it up next year.

But I do think I helped them to KNOW, you know?

Developing the standard rule of an ellipse

This activity was inspired by two people: Teresa Ryan, a fabulous math teacher tweep, and Amanda R., one of my students. A few days ago, Theresa tweeted this

Anyone have a good introductory lesson to the standard form of the equation of an ellipse? TIA #MTBoS #mathchat
— Teresa Ryan (@geometrywiz) May 7, 2014

and that question started the cogs turning. Around the same time, I had my students playing around with circles on desmos. Amanda happened to type in the equation 2x² + 2y² = 1, and notice that it had a smaller radius than our unit circle. That lead to a nice discussion as to why the radius was less than one, and then why it was equal to the square root of 1/2.

So today, again, all of this kind of gel-ed on my way into class. Here are my guiding questions, and their collective answers:

Open a desmos or ggb, and get the unit circle to show up.

Now type in 2x² + 2y² = 1. Tell me what you get, (smaller circle), what's the approximate radius? (0.7)

Type in another equation like this, which = 1, but make an even smaller circle appear, and write your equation on the eboard, plus the approximate radius.

Find pattern: as coeffs get bigger, circle gets smaller.

And what's the relation between the coefficient and the radius? Radius is the square root of one over the coefficient.

Okay, if bigger coefficients make smaller circles, what coefficients will make bigger circles? (1/2 or 1/3)

Type those in, measure the approximate radius, and write on eboard:

Is it okay if we write these equations this way instead? Are they equivalent?

Now how can we calculate the radius from the rule? It's always the square root of the number in the denominator.

Which denominator? Well, it doesn't matter. Doh. They're the same.

Oh right. I didn't notice that. Well type one in that doesn't have the same number under each term, what do you get? An ellipse!

Tell me your equations and the dimensions of your ellipses:

Unfortunately I didn't take a snip of this, but the variety was wonderful, some ellipses were horizontal, some vertical, it was absolutely no big deal for them to see that the number under the x always governed the width and the one under the y governed the height, plus that a square rooting was involved.

From there it was a piece of cake to generalize to the standard form of the ellipse! We did a bit of practice where I gave them the rule and they graphed, and vice-versa. It felt like I'd covered 2-3 days' worth of concepts just today.

Thanks Teresa and Amanda!

New Intro to Locus and Circles

All of this actually happened today, although, well, maybe not all during the same class. So it's piece-wise true...

Part 1: Locus intro:

This was the first day of our last chapter, conics. I wanted to begin with the idea of the locus of a point. But I didn't want to actually tell them what a locus is, I wanted to show them, then get them to tell me.

I got this idea on my way into class, which by the way there has to be something to why that happens so often at that exact time. Anyway, I thought of a use for one of my geogebras that was not at all what I had intended it for. This video explains what I had intended it for, and what I ended up doing instead:




By the way, if you're interested, here's that geogebra. Next I asked my students what they thought a locus was. Here are a few samples, word for word:

• The path of a point followed by a specific function
• a locus is the path a point takes
• The path of a point of a function
• The trace of a moving point

Their words, not mine. Which, collectively, touched on all of the key points - that it's a path, that it's created by a point, that the point is moving, that as it moves, the point is following some kind of rule.

Part 2: The circle as a locus:

I then wove all of these locus ideas into this geogebra, made by the brilliant Jennifer Silverman:
How beautiful is this?

I let them play with it a bit, to draw a few circles, then identify which of these virtual things was the locus, which was the moving point P, and what rule that point was following as it moved. Here are their answers, again collectively:

What is the locus? The circle is the locus! (Just that right there was huge. All these years I've been the one saying that, and approximately no one was really seeing the circle any differently than they had always seen it - as a static thing.)

Which point traced this locus? The point at the tip of the pencil.

What rule did the point follow as it moved? It stayed the same distance from the red pin.

Then we formalized that into the locus definition of the circle, which for the first time since I've ever taught it, I didn't have to dictate or get them to fill in the blanks on pre-made notes. Okay, I did give them the word equidistant.

Part 3: The rule of the circle

Next I wanted to move onto the Cartesian coordinate system, so we reviewed that:

• the rule for the unit circle is x² + y² = 1
• where that rule came from (right triangle inside circle)
• that really the 1 in the rule was 1².

 I gave them this desmos:  and had them work on that in groups. Just like when they're using geogebra, there is no need for me to tell them if they're right or not. If it is, they'll see a circle with the right radius. Again, there were no notes, no me telling them what the rule is. It took some trial and error, but eventually everyone noticed that the radius has to be squared in the rule. After a bit we regrouped, discussed, even a few things that I hadn't expected would come up:

• Why is the radius squared in the rule? Why isn't it just x² + y² = r?
• Is it possible to get a circle that's even smaller than the unit circle?
• One student noticed that  2x² + 2y² = 1 gave a smaller circle than the unit circle.  Why would that be?

On the way out, I had another idea. I need to write this down so I'll remember it all next year. That was 9 hours ago!