Why is it easier and cooler in the group environment? Usually, these summaries involve students using the offline GeoGebra, saving and numbering successive versions of their function summaries, sending each version to me, me downloading each version, me giving feedback on each version (using various tools completely separate from ggb, eg annotating a screen capture, or Camtasia video, or Smart Notebook etc) etc. But when it's all done in the group space there's no need for any of that - no saving, no numbering, no sending. And my feedback happens right there, in the same space as their work - right underneath it in fact, in a chat box, to which they can reply, also in the same space.
Here's what I did:
The Rollout:
The students login to our group at www.geogebra.org, where they see this post:
...in which they find out they'll be doing a GeoGebra task, then coming back to this post to make a comment right underneath it, in the public comment space.
To get to the task, they just click on the "Trig Function Starter Kit" and see this:
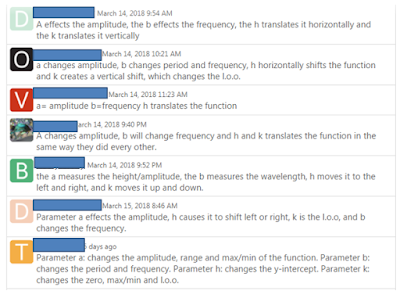
The task on the first day: Input one of the two wave functions, with all 4 parameters, and add the a, b, h, and k sliders to the worksheet, so they can start experimenting. They played around with the sliders until they were ready to post a comment in the public comments section about which property(s) is(are) affected by which parameter. I wanted the discussion to be public so that they feel part of a community of learners, and they can learn socially. Here is a screen capture of some of the comments as they appeared in the public space:
The Gathering:
They of course can all see everyone else's comments, but I wanted to rearrange them to give a different perspective. By the next day, I had sorted all their comments by function, student, and parameter, as you see below. This way they could see who went with which function, and who had already decided to go for the bonus point ("K" at the bottom - I suspect that seeing this caused many to do the same the next day!). They could also see, in one slide, that everyone agreed that parameter a changed the amplitude:
 |
| Parameter a |
This sorting also revealed that everyone agreed on b affecting the frequency....
 |
| Parameter b ....but the one below showed that not everyone noticed that b also affects the period. I love how some students extended their comment to explain why: "...how wide the waves are", "...bigger b = smaller period" This is another reason I like the discussion to be public - so that everyone gets their brain stretched. |
 |
| Parameter b |
The Dynamic Phase:
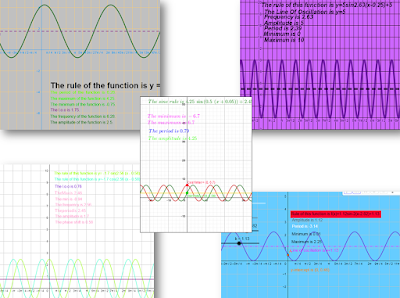
Next it was time for them to add dynamic info to their ggb: the line of oscillation, textboxes showing the max and min, amplitude, frequency, and period. I emphasized that since we'd already decided that, for example, b affected the period, then the textbox about the period should include some kind of formula involving b...and amplitude should involve a etc, and in fact, they'd already seen those formulas in a voicethread. So off they went to add to their ggbs. and I gave feedback in the private space. Lo and behold, there were mistakes aplenty, some of which I hinted at in my feedback. But I wanted them to be able to do their own detecting, to check their own formulas. So my next phase was...
Check Your Own Formulas Geez!
Next day in class, we spent a few minutes filling in this table from the text:
using what we already knew about how to find amplitude, period, maximum, and minimum. At this point they already, theoretically anyway, "knew" that amplitude = |a|, frequency = |b|, Max = k + |a|, etc. So this table was filled without geogebra, only math knowledge. Once we'd all agreed on the correct answers, and I'd done all the necessary intervention to make sure they were correct, I said ok - go to your geogebra and see if IT'S getting the right answers.....aaannnd....delightful flashlights ensued!
"oh no mine's giving -3 as the amplitude"
"mine says period is 2pi/3.5 how do I get it to actually calculate the period?"
"how do we set the b slider to pi/5?!"
Talk about differentiation, and just-in-time learning.
A Turning Point
This step was really important, and it's one that I've been aware I needed to improve on - to start with the math. Instead of students relying on the tech, I want the tech to rely on them. It's one thing to get an answer right, it's another thing entirely to cause someone else - or in this case something else - to get it right. This step also addresses my fear of digital dust - that once these beautiful works of geogebra art are handed in, they are never looked at again. Starting this class with this table exercise went some way to motivating them to use their own work, but first they have to OWN their own work, to TRUST it. And in the process learn how to empower and trust themselves.
This time my feedback took even less time. A lot of things had already been fixed. But I did notice that things were getting verrrrrrrrry colourful!
Building on solid ground
The next task, version 2, involved adding features that depended on all the formulas already established and working properly in the first version. For example, I wanted them to add a dynamic textbox about the domain and range. Range, of course, depends on the max and min values, for which they've already written and verified their formulas: max = k + |a| and min = k - |a|. They could therefore just say "range = [k-|a|, k+|a|], and let geogebra do the calculations.
Cool, but the absolute best part...
This came about because my students instinctively did something in a way that I totally did NOT anticipate, and it actually made a lot more sense from a pedagogical point of view. So they kind of taught me how to teach them.
I had also asked for a few "sticky points", including what I call the boc (beginning of cycle) and eoc (end of cycle). (Sticky points btw are what I call points that always stay in the right location on the graph eg a y-intercept that is always on the y-axis no matter how the parameters are changed. More on this here.) The boc would therefore stick to wherever a basic cycle began, and the formulas I had in mind were boc = (h, f(h)), and eoc = (h + period, f(h + period)), but one student, who had elected to do the sine function, said to me, Mrs, isn't the boc just (h, k)?
And I replied "no, but you're close", thinking that she was confusing vertex with boc.
And then one by one, my students, at least those who had also elected to do the sin function, thought about it, and said Mrs she's right. The sine function starts on the loo (note - that's what we call the line of oscillation), which is k. Then the cosine people started to ask well that's fine for you guys but what about the cos where does it start oh wait it starts at...the max oh ok. And one asked me privately "isn't that only if a is positive? If a is negative doesn't it start at its min? how do we do that in ggb?" And I, the teacher, who is supposed to know everything, didn't have an answer for her. Yet. It was awesome.
AND EVERYBODY LEARNED SOMETHING.
I had NOT anticipated anyone doing it this way - by using the key points (max, min, loo) that apply to the actual function they've chosen, and now I realize the HUGE benefit of doing it this way. It forces everyone to really look at the structure of the wave, that sin with a>0 is loo-max-loo-min-loo, cos with a>0 is max-loo-min-loo-max. And it's different when a<0. Next year....this will be in my improved game plan.
It's funny, I had originally let them do only one function, sine OR cos, because I didn't want to overload them, but it turned out to be a starting point for a deep discussion between two camps - the sine people and the cosine people. Once everyone's version 2's are all corrected and verified, I'll get to ask "Can anyone think of a formula for boc that would work for BOTH functions?" That'll be when boc = (h, f(h)) & eoc = (h+p, f(h+p) would have a bigger impact anyway. I'll also have them discuss which formulas are the same in both camps, and which are different. EEEEEEE I'm SO looking forward to that.
The advantage of the function summary in GeoGebra:
I maintain that getting them to do this task, to make something else work properly by using their math knowledge, is the closest I can get my students to becoming teachers, which, it is generally agreed, is the best way to learn something - by teaching it. They're kind of teaching geogebra what to say, what to look like, and where to put the points so they stick. And it's lovely. Each discussion that springs out of these tasks is richer and more meaningful because of the ownership, or maybe it's called agency now, of the work. And each discussion leads to other even richer ones, for example after the boc one, we moved on to the eoc, which of course will have an x coordinate that is one period further afield than the boc. But the path to a student realizing that is fascinating to watch, and talk about an aha moment. And who already has a verified formula for the period? My kids do.
The advantage of the marriage:
As I mentioned before, the flow is hugely improved. It's so many fewer steps, for all of us, to get the back-and-forth that's so valuable. I've always tried to set things up so that my students feel like I'm running the marathon alongside them, rather than just standing at the finish line with a red marker pen, but the way groups are set up, it's so much easier. This private convo:
...which happened in the group space would otherwise have taken at least 3 save/upload/download/give feedback/upload/download cycles and it wouldn't all have been in one place. To say nothing of the impact of the public forum on that social aspect of learning. I feel I've only just seen the tip of that iceberg.
