Just had THE most fabulous time with my grade 10's. It was the introductory lesson on congruent triangles, but I didn't want to say the words "Congruent triangles" and give anything away.
So I gave them this geogebra worksheet, created by Evan Weinberg. They moved the segments around to form a triangle, then took a snapshot using their snipping tool. Then they went to this googledoc to insert their snapshot. I made it clear that under no circumstances were they to shrink or enlarge their image, I wanted the actual size. After we got just a few of them inserted, I moved my own triangle outline over theirs, sometimes flipping, sometimes rotating, and lo and behold, we all had the same triangle. So sss demonstrated without words, only by doing and comparing.
Next, they all logged onto their explorelearning accounts, and started the Proving Triangles Congruent gizmo. Did a quick demo of how to measure sides and angles, how to select the conditions, and how to play around with the triangles to see if they are definitely congruent, or not necessarily congruent under those conditions. Then they worked in pairs to fill in the slides of this powerpoint, using snapshots from the gizmo to back up their statements:
I haven't even looked yet at their dropboxes to see how they did, but I am already struck by how many tools they are now comfortable using! Geogebra, snipping tool, googledocs, explorelearning gizmos, powerpoint, uploading to the CMS.....I just spoke with some McGill students last Tuesday night about, among other things, all these cool tools I and my students use, and one of them asked me if the kids ever get overwhelmed by all of them. I said I didn't think so, because I hadn't heard any complaints. but after today, I am convinced they are fine! At least with the half a dozen or so we used today, because they seemed to just click right along, in fact, some had even started it BEFORE class!
We'll see how it goes, but one way or another, it turned out SO much better than I thought it would. Maybe I'm not crazy after all!
Thursday, March 1, 2012
Friday, February 24, 2012
Immortals in my class - who knew?!?!?
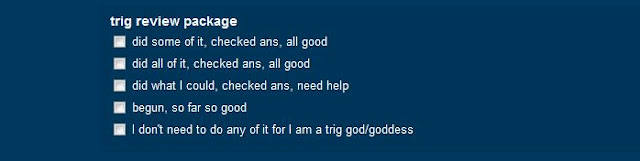
I have been getting really cheeky lately with my checklists. Maybe I'm just tired of seeing the same 2 or 3 possible answers, which means the kids are too. But I do like to amuse myself too! Here are a few samplers:
Desperate for comments on the voicethreads:
Desperate for comments on the voicethreads:
....and it looks really funny at the end of the week, like they're all yelling at me!
Just curious who might notice this AND check it off:
....and they practically all did!
Aaaaaannnnnnnd I am just so sarcastic sometimes it is surely wrong:
Apparently there are several trig gods in my class, but sadly so far, no goddesses. Well, heaven help them, they had better be prepared to prove it.
Anyway, perhaps I should start calling them cheeklists.
Graphing trig functions using google drawings ..... and a box
I have developed what I think is a fun and easy way for my kids to graph a decent trig waveform by hand. I have always felt that actually graphing a few sine and cosine functions helps to understand the properties that only pertain to trig functions, like period and line of oscillation. This activity has been adapted many times over the years, and this time, it's in the cloud!
The basic steps of the graphing procedure:
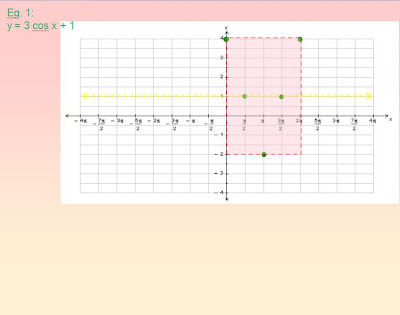
They warm up by placing 5 key points inside a box, any box, like this, eyeballing it so that the 2nd, 3rd, and 4th points are halfway between everything else vertically and horizontally:
Then they join those as smoothly and curvey-y as possible:
Once they can do this in any-sized box I give them, they just have to do it on the cartesian graph. Which means THEY have to first draw the box.
So next, they calculate the correct locations of the box's corners on the cartesian graph. This is about 25 slides condensed into two:
Now they can place the 5 key points in this box, which just happens to be on a real grid:
The basic steps of the graphing procedure:
They warm up by placing 5 key points inside a box, any box, like this, eyeballing it so that the 2nd, 3rd, and 4th points are halfway between everything else vertically and horizontally:
 |
| 5 key points |
 |
| One cycle of the cosine function |
So next, they calculate the correct locations of the box's corners on the cartesian graph. This is about 25 slides condensed into two:
 |
| Use max and min to get top and bottom of box |
 |
| Use phase shift and period to get left and right ends of box |
This makes it pretty easy to repeat and draw as many cycles as they want:
Of course we then extend to the sine curve, and then to using a regular x-axis, as opposed to one with all those π's all over it.
So how did this go into the cloud?
First I put the above procedure on a voicethread, which they were to watch at home. Then I put some practice examples onto a googledocs drawing, like this. Next day, in class, I gave the students the link, did a quick demo of two tools: the rectangle tool, and the scribble line tool, and we were off to the races.
So how well does it work?
As usual, my answer is...........it depends. If you measure the success by how much fun they had and how engaged they were, it was pretty successful. Lots of laughs (or lols) at how wobbly some curves were! I was also able to correct some mistakes right off the bat because I could see what they were doing as they were doing it, so as an intervention, it was also successful. As a collaborative activity, it was so-so, for as usual I decided who would work with whom. As a pure practice activity, not bad, only had time to do two functions, and I had prepared 4. I'm pretty sure the slowness was not because of the tech, though, it was more about them being at the beginning of their trig curve-learning curve.
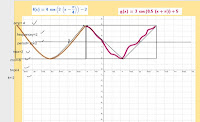
And the graphs? Well, I believe in full transparency, so here's their work, warts and all, (just a figure of speech, I think they are gorgeous)::
First I put the above procedure on a voicethread, which they were to watch at home. Then I put some practice examples onto a googledocs drawing, like this. Next day, in class, I gave the students the link, did a quick demo of two tools: the rectangle tool, and the scribble line tool, and we were off to the races.
So how well does it work?
As usual, my answer is...........it depends. If you measure the success by how much fun they had and how engaged they were, it was pretty successful. Lots of laughs (or lols) at how wobbly some curves were! I was also able to correct some mistakes right off the bat because I could see what they were doing as they were doing it, so as an intervention, it was also successful. As a collaborative activity, it was so-so, for as usual I decided who would work with whom. As a pure practice activity, not bad, only had time to do two functions, and I had prepared 4. I'm pretty sure the slowness was not because of the tech, though, it was more about them being at the beginning of their trig curve-learning curve.
And the graphs? Well, I believe in full transparency, so here's their work, warts and all, (just a figure of speech, I think they are gorgeous)::
I thought they were pretty terrific, in fact, quite consistent, all things considered. I displayed them the next day to each group so they could compare, and it was interesting to hear the reactions. Some were impressed with how smooth some people were able to get their curves. One group's curves were a little too perfect, actually:
But they had found a way to follow the procedure AND improve on it! They had done their calculations and drawn the box, but found that by using the curve line tool instead of the scribbler, and hitting only the max and min, the curve automatically went through all 5 key points, and it looked beautiful! Which suggests to me that there must be some trig involved in the curve line tool.....so I learned something too!
A few organizational details:
- When creating the practice activity, I went with the google drawing because I couldn't find the scribble tool on any other type of googledoc, but now I see that it's there in "Presentation" too.
- I didn't have everyone working on one google drawing at the same time, because it tends to be too slow with that many people. I made a few copies and split the kinds into groups of 2 or 3.
- Each of the copies' file names contained the names of the kids in that group, to help me keep the picture in my head of who was working with whom. I need a lot of help, what can I say.
- When sharing, I set it so that everyone with the link could edit it, otherwise no one would be able to draw!
- Since they were all still in the virtual class during all this, I put them into breakout rooms according to their groups, so that I could talk to one group at a time if needed.
- I had them write their calculations on the classroom whiteboard instead of the google drawing. The scribbler is just terrible for writing. That also kept their graphs relatively clean.
- While they were working, I was able to click from tab to tab and quickly know which group I was looking at because of the names in the file title.
Next time:
- I'd like to add some suspense to it - maybe they are initially working on individual cycles, but they get stuck together so that in the end, if everyone has done it right, we get a nice long graph with lots of nice smooth sort-of-identical peaks and troughs. Everyone contributes to it, but only at the end.
- More examples, and widely varying box sizes, just for fun. One really tall, skinny one, and one that is the width of the entire google drawing!
Wednesday, February 22, 2012
Confessions of an un-cooperative learner
Now that I have come full circle with flipping, that is to say, it has been a year since I started flipping, I can use some of the voicethreads and videos I used last year. Punched up a bit of course, but it should get a bit easier to be prepared. Which means I can focus on the class activities, to make them more interesting, collaborative, and authentic.
How can I ask kids to do something I wouldn't want to do?
The collaboration part is the hardest for me. I have always struggled with putting kids into groups, probably because I have never liked working in groups myself. As a young teacher (which was just last week....) I was decidedly uncooperative about cooperative learning! I guess I wouldn't make a very good dolphin. They clearly do everything in cooperative groups.
I think part of the problem is that it all seems so un-authentic to me. Whenever I was put into some group for a workshop, I thought "Why should I work with people that I don't know and would ordinarily not want to have anything to do with, and who don't seem any more jazzed about this than I am?" So I know how the kids feel. And even if the kids DO want to work with someone else, THEY should be choosing who it is, not me. And then there's the task, which always seemed so contrived, like pretend you are organizing this, and your task is to do that....enough pretending already.
But my inner dolphin is emerging!
Our team at Learn did a fabulous group presentation last week at LCEEQ, which was clearly greater than the sum of its parts, so I get it now. And I watched this video a while ago that got the cooperative ball rolling:
I recognize fully that learning is a social activity, or at least it should sometimes be. So I have been trying to come up with ways to just get groups to form organically. Kids wanting to work together because of an authentic reason that doesn't involve marks, or teacher direction, or pretending. And like most things, the ideas come to me when I am not particularly looking for them, or ready for them.
The other day in my grade 10 class, this happened:
Two kids who are always ahead of everyone else, which is to say, they do things on time, and they are both very strong students, both happened to have questions on the same assigned textbook examples. Wanting to be efficient, I took them into a break out room to help them both out, just trying to save time. I gave a bit of help, then I got an idea. I proposed that they just stay in that room together since they're working on the same thing, and they might be able to help each other out. They were ok with it. Then I left, and returned a few minutes later, without them seeing that I was back (ZENlive, our virtual classroom, has many tricks like that) ....and they were actually working together, discussing, asking, writing on the board. And when class was over, they stayed there to finish the work!
Then a few days later, in my grade 11 class, this happened:
Exactly the same setup, but this time, five students. When I went back in to check, nothing was happening. :( What was different: this was a group of five, not two. That might have been all there was to it. But the task was also a lot easier, so there was no compelling reason for them to collaborate. And I explained it all.
So here's what I'll do next time:
Plant a seed in the assigned work that will get a lot of questions to lure them in, then put them in a group, and then shut myself up! I'll just say here, you guys all have the same question, see if you can put your heads together. Good luck, get cracking.
Me tell you? What do I look like, a dolphin?
How can I ask kids to do something I wouldn't want to do?
The collaboration part is the hardest for me. I have always struggled with putting kids into groups, probably because I have never liked working in groups myself. As a young teacher (which was just last week....) I was decidedly uncooperative about cooperative learning! I guess I wouldn't make a very good dolphin. They clearly do everything in cooperative groups.
 |
| I wonder if there's a dolphin off-camera thinking "Meh." |
But my inner dolphin is emerging!
Our team at Learn did a fabulous group presentation last week at LCEEQ, which was clearly greater than the sum of its parts, so I get it now. And I watched this video a while ago that got the cooperative ball rolling:
I recognize fully that learning is a social activity, or at least it should sometimes be. So I have been trying to come up with ways to just get groups to form organically. Kids wanting to work together because of an authentic reason that doesn't involve marks, or teacher direction, or pretending. And like most things, the ideas come to me when I am not particularly looking for them, or ready for them.
The other day in my grade 10 class, this happened:
Two kids who are always ahead of everyone else, which is to say, they do things on time, and they are both very strong students, both happened to have questions on the same assigned textbook examples. Wanting to be efficient, I took them into a break out room to help them both out, just trying to save time. I gave a bit of help, then I got an idea. I proposed that they just stay in that room together since they're working on the same thing, and they might be able to help each other out. They were ok with it. Then I left, and returned a few minutes later, without them seeing that I was back (ZENlive, our virtual classroom, has many tricks like that) ....and they were actually working together, discussing, asking, writing on the board. And when class was over, they stayed there to finish the work!
Then a few days later, in my grade 11 class, this happened:
Exactly the same setup, but this time, five students. When I went back in to check, nothing was happening. :( What was different: this was a group of five, not two. That might have been all there was to it. But the task was also a lot easier, so there was no compelling reason for them to collaborate. And I explained it all.
So here's what I'll do next time:
Plant a seed in the assigned work that will get a lot of questions to lure them in, then put them in a group, and then shut myself up! I'll just say here, you guys all have the same question, see if you can put your heads together. Good luck, get cracking.
Me tell you? What do I look like, a dolphin?
Friday, February 3, 2012
Start with the students
Here's what I've been doing since my last post, wow, almost a month ago, just shows how productive I've been, if I do say so myself:

More detail to come, but feel free to comment or give feedback, either right in the voicethread, or here!
- got student blogs going
- got class blog set up, and all of their blogs are linked to it
- tried out and LOVED in-class live collaborative editing using googledocs
- fixed it so that during this live editing we can all see each others' names next to our cursors (instead of "anonymous user")
- added students as googledocs contacts, in groups by course (that was how to do the above)
- set up "form emailer" - so that as soon as kids submit something to the checklist, they will receive an email listing everything they checked off/said (got that from the script gallery at gdocs, my new favourite shopping place)
- started using my gmail account finally - mainly because it's the only one my groovy new smartphone will allow me to look at for now
- geogebra - made tons of new worksheets, including ones with sliders and conditional colouring
So now I have to post in more detail about all this, in case there is anyone out there who wants to know how to, or just see how all these things look and feel. That should take.....a while. But here goes. Starting with the blogs:
Student blogs and class blog:
Before I could set this up, I had to get a big picture. Like some sort of structure of the blogs, who do I want linked to whom, how would it look, how do I start....I got really hung up on that. Then my fabulous fellow online teacher Paul told us about how he did it with his history students, and it all became crystal clear. Start with the students. Have them create their own blogs first, if they don't already have one. This is just a sort of pictorial representation of how it all looks in my wee head:
More detail to come, but feel free to comment or give feedback, either right in the voicethread, or here!
Labels:
blogs,
class blogs,
form emailer,
geogebra,
gmail,
googledocs
Wednesday, January 4, 2012
First McSquared-iversary
Today is exactly one year since I posted my first deep thoughts on this blog. Now my blog archive has a link for 2011 and 2012 - cool! Might as well call it Audrey 2011 and Audrey 2012, because this year I have learned, wondered, and lived right here on McSquared.
Did I do what I wanted?
My original idea for this blog was more or less centered around online teaching, and by that I mean REALLY online - the virtual, live classroom in which I teach. But 99% of what I learned and blogged about applies to any classroom. So my goal is a subset of what I ended up doing. Check!
What did I learn?
Specific tools: Voicethread, googlereader, googleforms, googledocs, geogebra, twitter, self-correcting quizzes, Camtasia studio, blogger, wordpress, codecogs, voki, and just started learning javascript!....embedding any of these in blogs, facebook, google+, countless combos of them all. In terms of teaching strategies: class blogs, flipping the class, Malcolm Swann activities.
The Big Picture: What I learned about me:
I need to blog.
I need to be creative.
I need to share what I've learned.
I need to share how that makes me feel.
I am in charge of 30 young people who also need those things.
Doing all this soul-searching in public is hard.
Doing all this soul-searching in public is easy.
I am jealous of people who get a bazillion comments whenever they post on their blog.
I need to comment on other peoples' blogs, whether or not they already have a bazillion comments.
It really is important to answer all comments on your post.
It really is wonderful when someone else answers your comments on their post.
Sometimes you can predict when you'll get a lot of reads.
Sometimes you can't - The Wizard of OZ?!?!?
When I am writing a post that really gets me, it is all can think about until I am done.
When that happens, I don't know if three minutes or three hours have gone by.
But my kids sure do. (The biological ones, I mean.)
Any future potential employer can read my blog before the interview and have a pretty good idea of who I am as a teacher and a person.
Any future potential employer that doesn't do that might not be an ideal employer for me.
An awful lot of people out there think people who blog are egotists.
I would much rather change that than be hurt or complain about it. Even if it comes from friends and family members.
An awful lot of people out there are afraid of technology.
I am still one of them (btw posting about my new smartphone really, really soon).
I have never read so much, written so much, struggled so much, learned so much, or grown so much as I have in this last year. And all because I was free to pursue my interests.....I wonder what would happen if my students had that opportunity?
One year from now, who knows? I'll just keep doing what I'm doing, and like Dorey says:
Did I do what I wanted?
My original idea for this blog was more or less centered around online teaching, and by that I mean REALLY online - the virtual, live classroom in which I teach. But 99% of what I learned and blogged about applies to any classroom. So my goal is a subset of what I ended up doing. Check!
What did I learn?
Specific tools: Voicethread, googlereader, googleforms, googledocs, geogebra, twitter, self-correcting quizzes, Camtasia studio, blogger, wordpress, codecogs, voki, and just started learning javascript!....embedding any of these in blogs, facebook, google+, countless combos of them all. In terms of teaching strategies: class blogs, flipping the class, Malcolm Swann activities.
The Big Picture: What I learned about me:
I need to blog.
I need to be creative.
I need to share what I've learned.
I need to share how that makes me feel.
I am in charge of 30 young people who also need those things.
Doing all this soul-searching in public is hard.
Doing all this soul-searching in public is easy.
I am jealous of people who get a bazillion comments whenever they post on their blog.
I need to comment on other peoples' blogs, whether or not they already have a bazillion comments.
It really is important to answer all comments on your post.
It really is wonderful when someone else answers your comments on their post.
Sometimes you can predict when you'll get a lot of reads.
Sometimes you can't - The Wizard of OZ?!?!?
When I am writing a post that really gets me, it is all can think about until I am done.
When that happens, I don't know if three minutes or three hours have gone by.
But my kids sure do. (The biological ones, I mean.)
Any future potential employer can read my blog before the interview and have a pretty good idea of who I am as a teacher and a person.
Any future potential employer that doesn't do that might not be an ideal employer for me.
An awful lot of people out there think people who blog are egotists.
I would much rather change that than be hurt or complain about it. Even if it comes from friends and family members.
An awful lot of people out there are afraid of technology.
I am still one of them (btw posting about my new smartphone really, really soon).
I have never read so much, written so much, struggled so much, learned so much, or grown so much as I have in this last year. And all because I was free to pursue my interests.....I wonder what would happen if my students had that opportunity?
One year from now, who knows? I'll just keep doing what I'm doing, and like Dorey says:
Tuesday, January 3, 2012
The activity that became a class that became an assignment...and next?
I have been developing something over the years that I call The Big Picture. It started as a classroom activity, from way back when I was teaching in a brick-and-mortar class, so we're talking at least 5 years ago, probably more like 8. This is the first year that I have used it as an assignment, and it really seems to be....I don't know, becoming something.
Long ago, in a grade 11 class far, far away:
Once we had done a few different functions, I would put this on my beloved smartboard (btw, miss you! love you!)
Usually, someone would assume I meant the function we had just done, but on a good day, another person would say "What type of function is it though?" and I would rejoice! Just that moment felt like a breakthrough - ooooooh it could be ANY function!
"Quadratic" I would say. Much unhappiness...ummm miss, we did that LAST year....hello, we're like 16 now.
Once I beat them into submission, we would get an equation that did indeed pass through the two points, like this:
Looking at a bigger picture now:
I said "Is there any other quadratic function that goes through these two points?" Which brought us to the idea that there could be at least 2, depending on which one is the vertex. And on a great day, we would get into "What if neither of them is the vertex?", and how there are infinitely many possible answers, because that's how many parabolas you could draw through those two points if neither one is the vertex.
Since my first career choice was acting....
I would then smack my forehead, and exclaim "Wait a minute! Did I say quadratic? Wow, you guys are like 16, whoah, sorry, my bad, I meant it was an absolute value function!" Knowingly rolling their eyes, they would tuck into that.
And a bigger picture would emerge:
Because now it was time to talk about a bunch of other stuff, like: compare your method for finding this rule with the quadratic? do you expect any of the parameters to be the same? which and why? are you making any assumptions this time?
After we had done the absolute value and all its possibilities, I did the head-smacking thing again, they rolled their eyes again, only to be shocked that now I was "realizing" I actually wanted a linear function that went through these same two points.
Blink. Miss. That's, like, insulting. Oblige me, I would say, and after a quick review of slope, etc:
But then when I asked the same questions as before, like is there any other possibility, which is the vertex, compare methods, parameters, etc there was some wonderment. And on a great day, someone would notice that the slope matched part of the absolute value function....coincidence?
The big picture that day was:
When all went well, and I had enough of them hooked to reach critical mass, they could see that if there is enough information to DRAW only one function, that means there is enough information to find one and only one rule,and also that any time you are making assumptions about which function, which vertex, etc, your answer must include those assumptions. But I didn't want to say it! I wanted them to!
And that's it, right, no bigger pictures out there?
Well, that's the thing. From there, each year, I added more and more functions, and more and more questions, so that it evolved into something that got too big to do in one class, so I split it up into 2, then 3, so that I had a sort of cycle going, where after finishing a unit or 2, I would do a Big Picture class, and everyone got to know what that meant. But even that changed each year.
This year, with geogebra, it's all been ramped up about 20 pegs. Now they get to be the ones typing their rule into the input, and seeing if they get something that goes through the given points. Instant feedback of the most authentic kind. They also get to colour things in! Which is hugely motivating, as it turns out, not really surprising, as I love to make things look nice too.
So currently, it is an assignment that comes in two parts, the geogebra part, which they get here on geogebratube, and a list of exploration questions in this word document.
But I'm still the one asking all the questions, which is where I hope the next change will come from. Just because I love the connection between the drawing and the algebra doesn't mean they do. Already in some of their work, I have read things that I never thought of, which is absolutely thrilling. And humbling. And enlightening.
As soon as all parent permission forms are in, I will post some of their work, which was astonishing, to say the least!
Happy New Year, can't wait to see what we'll all be doing/sharing/thinking one year from now!
Long ago, in a grade 11 class far, far away:
Once we had done a few different functions, I would put this on my beloved smartboard (btw, miss you! love you!)
Usually, someone would assume I meant the function we had just done, but on a good day, another person would say "What type of function is it though?" and I would rejoice! Just that moment felt like a breakthrough - ooooooh it could be ANY function!
"Quadratic" I would say. Much unhappiness...ummm miss, we did that LAST year....hello, we're like 16 now.
Once I beat them into submission, we would get an equation that did indeed pass through the two points, like this:
Looking at a bigger picture now:
I said "Is there any other quadratic function that goes through these two points?" Which brought us to the idea that there could be at least 2, depending on which one is the vertex. And on a great day, we would get into "What if neither of them is the vertex?", and how there are infinitely many possible answers, because that's how many parabolas you could draw through those two points if neither one is the vertex.
Since my first career choice was acting....
I would then smack my forehead, and exclaim "Wait a minute! Did I say quadratic? Wow, you guys are like 16, whoah, sorry, my bad, I meant it was an absolute value function!" Knowingly rolling their eyes, they would tuck into that.
And a bigger picture would emerge:
Because now it was time to talk about a bunch of other stuff, like: compare your method for finding this rule with the quadratic? do you expect any of the parameters to be the same? which and why? are you making any assumptions this time?
After we had done the absolute value and all its possibilities, I did the head-smacking thing again, they rolled their eyes again, only to be shocked that now I was "realizing" I actually wanted a linear function that went through these same two points.
Blink. Miss. That's, like, insulting. Oblige me, I would say, and after a quick review of slope, etc:
But then when I asked the same questions as before, like is there any other possibility, which is the vertex, compare methods, parameters, etc there was some wonderment. And on a great day, someone would notice that the slope matched part of the absolute value function....coincidence?
The big picture that day was:
When all went well, and I had enough of them hooked to reach critical mass, they could see that if there is enough information to DRAW only one function, that means there is enough information to find one and only one rule,and also that any time you are making assumptions about which function, which vertex, etc, your answer must include those assumptions. But I didn't want to say it! I wanted them to!
And that's it, right, no bigger pictures out there?
Well, that's the thing. From there, each year, I added more and more functions, and more and more questions, so that it evolved into something that got too big to do in one class, so I split it up into 2, then 3, so that I had a sort of cycle going, where after finishing a unit or 2, I would do a Big Picture class, and everyone got to know what that meant. But even that changed each year.
This year, with geogebra, it's all been ramped up about 20 pegs. Now they get to be the ones typing their rule into the input, and seeing if they get something that goes through the given points. Instant feedback of the most authentic kind. They also get to colour things in! Which is hugely motivating, as it turns out, not really surprising, as I love to make things look nice too.
So currently, it is an assignment that comes in two parts, the geogebra part, which they get here on geogebratube, and a list of exploration questions in this word document.
But I'm still the one asking all the questions, which is where I hope the next change will come from. Just because I love the connection between the drawing and the algebra doesn't mean they do. Already in some of their work, I have read things that I never thought of, which is absolutely thrilling. And humbling. And enlightening.
As soon as all parent permission forms are in, I will post some of their work, which was astonishing, to say the least!
Happy New Year, can't wait to see what we'll all be doing/sharing/thinking one year from now!
Subscribe to:
Posts (Atom)