Another First in My 30th Year of Teaching

Welcome to the continuing saga of how I, in my 30th year of teaching, am doing things that I should have been doing for all these 30 years. Today's practice that I'm embarrassed to admit I'm only starting to do now is having students present to the class.  I'm not sure why I avoided it up till now, but I definitely know why I wanted to start very much this year. I was inspired by my colleague Peggy Drolet, whose classroom management skills I learn from every day. She and I both teach online, and so constantly have to work hard just to create a sense of community, establish our presence, and get the kids to do the same. A couple of weeks ago, she had her students do class presentations, with great success, and so I jumped on it. The presentations were, at least on the surface, about math, but I had lots of other ulterior motives - mostly social ones, as did Peggy.

Topic for Presentation:

We're studying optimization, so for a presentation topic, I chose the polygon of constraints. I always compare the pgoc to a sculpture, so I thought this might inspire some creativity. The constraints do the same thing as a sculptor's knife - they remove something so as to let the shape emerge little by little. I asked my students to design their own pgoc from their own constraints. The requirements for the pgoc were that:

• it be in the first quadrant
• it be composed of at least 3 constraints
• one constraint be in the standard linear form
• one constraint be in general linear form
• the slides be designed so that the shape of the polygon emerges one step at a time, slide by slide, with the resulting pgoc clearly outlined in the last slide, like this: 

Each constraint takes another slice off

The Medium:

Also inspired by Peggy, I had them create their presentations using Google Slides, so that I could watch them working live, and so that they could work outside of class time without having to actually be in the same place, which would have been impossible considering they're scattered all over the province of Quebec. I've had my students do activities using google slides before, but it was always something I had created, and they were to edit. Also, in the past they were able to access the slides without signing in, so I didn't know exactly who was in which document. This time it was all done through their GAFE accounts. No more anonymous bobcats or chupacabras.

Day 0: The Set-Up

I created a bunch of blank google slide documents, one for each team. I shared each doc according to who was on that team,via their emails. I had considered getting them to do this part themselves, which would have probably taken a whole day in and of itself, but I caved to save time. Plus, this way, since I was the owner, I also had immediate access to their slides, which I wanted because I want to be able to watch them work.

Day 1: Meeting in the Cloud

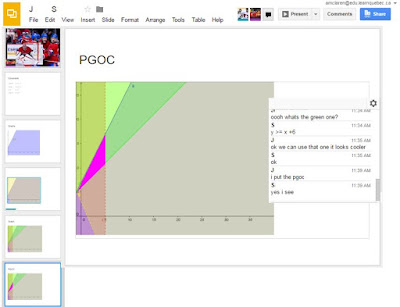
I described the project to the whole class, told them they had 3 days, then they just clicked on the links I'd shared via email, and boom, they were all in their respective presentation work spaces, with their team members, and I was sitting there waiting for them all. I had all of the files open at the same time on my screen, so I could just click one tab after another, and go from team to team to watch. This is what mission control, aka my screen, looked like:

At the top you can see all the tabs, with the names of team members visible. The tabs are just the file names, which, since I created them, I chose a title that made my life easy.

If I clicked on any one of the tabs, here's what I'd see:

I could see who was in the doc, which slide they were currently looking at, their live edits, and the live chat. It was really fun to watch them creating their pgocs while they were chatting using Google's live chat tool, which is right there in the same window. It was such an eye-opener to see how much they enjoyed collaborating, socially and mathematically. I feel like I benefited from knowing this at least as much as they did experiencing it.

But it wasn't only there that things immediately felt different. There was more communicating happening everywhere. That first day: "Bye guys, have a great day!" to the whole class, from kids who'd NEVER said anything like that before. Kids who'd never tweeted suddenly started to. I definitely noticed a difference in the social atmosphere - in and out of class - right away.

Days 2-3: Riches:

The math:

• Some groups needed help getting their constraints to match the pgoc they wanted, and some needed intervention in their work due to mistakes, so that was a classic just-in-time teaching opportunity. This felt like productive struggle.
• I got to deepen one group's understanding of solution sets: They had their pgoc ready and looking the way they wanted, and their constraints matched the pgoc, but they asked me to help them rewrite one of their constraints. It was in the form  y > -x + 7, but they wanted to put it in general form because that was one of my requirements (I'll make sure to include that next year too). They wanted it written in a different form, but they didn't want it to change how the pgoc looked. What a teachable moment! These are kids who've solved a ton of linear inequations before, but never realized that the algebraic steps they'd been doing actually didn't change the solution set. They were surprised, and relieved, to learn that x + y > 7 had the exact same graph as y > -x + 7.
• The usual benefit of teaching something - it helps you understand it better. I could literally see it happening before my eyes as they would find a mistake and fix it. Also, the task of organizing a large amount of info, for example all the systems of equations that define the vertices, gave them a bigger picture of the problem.
• The sheer variety of the inequations - not only did they go with standard and general, but also symmetric! Also things that don't really fit into any category, like 3x + 1 > 10, or 12 ≥ 3x + 4y, with the variables on the right side. I plan to use their actual constraints as a jumping off point for even more complex ones.

So many other cools:

• One group asked if they could include a quadratic inequation, which technically doesn't make a polygon, but which was definitely thinking outside the box. So I said yes!
• Creativity! One group decided to make their pgoc perfectly symmetric.
• One group organized themselves as follows: X designed the entire pgoc, Y found all the vertices, and Z created the slides for the presentation. That seemed like a pretty fair distribution of labour.
• Total GeoGebra and Desmos fluidity. I didn't have to help anyone with these tools, they just ran with it. The tools have become transparent.

Presentations: The PGOCS

I'm just going to let the pics speak for themselves. (I know there's a way to get blogger to put images side by side, but I can't even right now.)

Such style, such pizzazz!

As for the actual live presentations? So much fun to watch - how they handled it, and how the others reacted. Voice is a huge presence for anyone who teaches or learns in an online class. So much personality is revealed in the tones of a person's voice. Not to mention the little touches some added, like getting the others to participate, and putting little jokes in their slides. Everybody got to know everybody else a bit better, which for me, was the whole point.

My only problem was that I tried to record them all and chop the video files into individual ones, and in doing so, inadvertently deleted some. I could definitely use a digital assistant. This seems to be happening a lot lately. Must also have something to do with being in my 30th year of teaching....

But for sure, I'll be doing this in my 31st year too!

The Classic Homographic

Why I love rational applications:

Rational applications are worth spending more time on than absolute value or square root ones, I find, because they can harness so much algebra AND reality in one single problem. I spent two unhappy years working as a cost accountant, in which this type of problem came up a lot, and it was the only fun part of the job. So I'm giving my kids an assignment that's only on rational application problems, and in order to prepare them, I showed them 3 type of situations that they could expect:

1. The Constant Product situation:

This is the simplest one, in which the two variables involved always multiply to give the same result. They may notice this from inspecting a table of values:

Or by reading between the lines:

In either case, the relationship between the variables can be expressed as xy = a, or y = a/x, in which a is the constant product.

2. The cost-per-person situation:

In which there are two types of costs involved - a fixed and a variable (which I happen to know is how they're referred to in the cost-accounting world):

The fixed is the $3000, and the variable is the $750. The calculation that naturally occurs to students to make is the cost per person, and coming up with a rule for cost per person is fairly easy for most.

The fact that no person can ever pay exactly $750, but always slightly more, makes the concept of asymptote very real. This is a really nice intersection between their intuition and the very abstract concept of asymptotes.

Next level up would be a situation that involves something per something other than cost and people, but which has both a fixed and a variable quantity.

3. The Class Homographic

The name for which only occurred to me moments before I went into class - in which two linear quantities are being divided, so that the resulting function is rational, but its asymptotes would need to be discovered via long division:

Now this is where some really beautiful intersection between algebra and reality happens. They do the long division, which reveals the asymptotes, one of which is at 1000. So is that truly the maximum? Time to discuss. Not to mention that this is a great argument for doing long division in the first place, because it reveals so much about the nature of the function.

Next level up is a situation in which the homographic rule is not given, but two linear relations are, and they need to be divided, for example, the concentration of a solution in which the amount of solute and the amount of solution are both changing linearly.

How will this help them?

So often I hear - Mrs. - I don't even know where to start. Well, we spent the rest of the time looking at other problems and identifying which of the three types each was - which can help point the way.. Which I hope will help them with their assignment - we'll see on Friday when it's due.

At any rate, I just love how Classic Homographic sounds!

How to Get Organized in Your 30th Year of Teaching

Many years ago, as a young, disorganized, overwhelmed, but still enthusiastic teacher, I fantasized about opening up my plan book in September and having every lesson on every page already filled in. A stress-free year, in which I'd never have to wing it. I was so wrong about many things, not the least of which was that that would be a truly dull and cognitively dead classroom where nothing surprising or unexpected ever happened. But I was right about one thing - I did need to get organized, so that I could handle those surprises.

I tried a few things - colourful filing systems, getting advice from my mentors, just plain disciplining myself, with some small success, but everything seemed to require that I practically change my personality. Just stay up-to-date and keep everything neatly filed - it's as easy as that! It was meant to help but it didn't, not in any long term way.

Turning Point #1:

Sometime around 2002, my school got Smart Boarded, to my great delight. And say what you will about Smart Boards, but they helped me get organized.  I didn't expect that to happen, and it didn't happen right away - it took a year from the time I started using one. During that first SB year, I wrote on that fancy board much the same way I'd written on the chalkboard, but the biggest difference was that I could save all of that writing by date, topic, whatever I chose. That meant that I began the next year already possessing a real timeline for each unit, not to mention a starting point for planning better lessons for this year. In one stroke, my organization and pedagogy were improved and I hadn't had to suddenly change anything I was already doing in order to achieve it. I used what I did, and built on it. I think that's the key to getting organized - be who you are, watch what you do, keep a record of what you do, & build on that.

This year, I used some of what I'd learned from the SB years, plus I intentionally made one very small but powerful change.

Turning Point #2: The Small But Powerful Change:

I took attendance every single day for every single class. Absolutely non-negotiable.

I didn't do it at the beginning of class, mind you, because that was always the reason I'd skipped it in the past, that it took away class time. So this year I did it right after class, while it was still fresh in my mind who'd been there. Unexpected bonus - if I couldn't remember whether or not a certain student had been there, that meant I hadn't interacted with that child. Not good, but good to know.

How did this become so powerful?

• I got addicted to how good that one simple change felt - always knowing that my attendance was up to date. The data alone didn't make the huge difference, not right away anyway, but it made me realize how badly I'd been feeling all those years when it wasn't up to date, and especially when it invariably got so far away from me that I was literally pulling numbers out of the air at report card time.
• I also got addicted to having a daily routine. I'm embarrassed to admit that I reached my 30th year of teaching without any kind of daily routine. Not good, but good to know.
• Both of the above gave me energy - or more specifically removed a ton of negative energy. No guilt, no cringing when I see my attendance book, no time wasted on "OMG where do I even start today?"
• It lead to what happened next.

Turning Point #3: Documenting my Organizational Routines

From the first day of this school year, I paid attention to myself. Every time I noticed myself doing something along the lines of management/routine/organization (corrections, time sheets, reading emails, etc), I jotted it down on a post it and stuck that within reaching distance of my chair. Very quickly I noticed categories emerging - things I did every day, once a week, end of a unit, so I transferred this info onto colour coded post-its:

This took time - I was finding time to do something I'd never done before. Which meant that my own behaviour was changing, not because I or anyone else was forcing it, but as a natural consequence of simply watching myself.

Next level up

These post-its started turning into checklists, like the ones the pilots in Sully used, that helped them stay calm and think clearly while the plane was headed for the Hudson river with 155 people on board. Nothing on the checklist directly changed the outcome, but indirectly it gave the pilots the mental energy they needed to focus on solving a problem.

And that's how I think my checklists, routines, and post-its are helping me this year.

Next levels up

I refer to the daily checklist once or twice a day. I've added things to it, and moved some onto the weekly.

Every Monday, and again every Friday afternoon, I go through my weekly checklist. I've added things to it, too, and moved some around.

These routines, which aren't static by the way,  make me feel stronger, less overwhelmed, and less stressed. They help me in the short term and in the long term. They're not the same as those endless to-do lists I used to make. These are much more long term, and their benefits keep on multiplying.

So is my life perfect now?

I can't honestly say I'm getting everything done exactly on time, but I can say that I know how far away I am from that goal. I can make the adjustments I need to on the fly, weigh the costs, and use written words and facts as a basis for my decisions rather than full-out panic.

I can say that I'm organizing my class time better - fitting in those wonderful WODB activities, even a couple of mini-contemplate-then calculates!

I can say that I'm more energetic, more likely to remember to deal with all those unexpected things, having new ideas more often, trying out more things, doing a much better job of rolling out GeoGebra (more about that in a future post) ...it just feels a heck of a lot better.

I can also honestly say that for the first time in my career, two months into the year, instead of feeling the ropes slipping away from me, and in spite of the fact that I've been sick since October 12, I feel, in my bones, that I'm still at the helm, and doing a good job of keeping us all moving ahead. Good AND good to know.

Crowd-Sourcing Brings Personality

Since I teach online, I can have a lot of students writing on the eboard at the same time. I've been using this to my, and their, advantage. Instead of getting everyone to do the exact same thing, I make sure to ask something in which there is potential for a variety of answers. I also get them to own their answers by putting their initials or name next to it on the board. Then we talk about the differences or similarities, or classify them, etc just try to use the variety to get a bigger picture much faster than they could get with one example at a time. Not to mention that attaching students' names to each answer, and then addressing them by those names, lends personality and life to the whole activity. Variety, big picture, personality: Win-win-win!

We did this the day after a GeoGebra lab, in which students used Jennifer Larson Silverman's Drawing an Ellipse GeoGebra to experiment with drawing ellipses using virtual string. I had them keep string length constant while moving the endpoints, then vice versa. It was concluded that:

• When you keep the string length constant, the distance between the ends of the string influences the shape but only in the length of the smaller axis - the longer axis remains the same.
• When you keep the string ends constant, changing the length of the string influences the shape of the ellipse in both directions
• the length of the longer axis is always equal to the length of the string.

Last night, their homework was to watch a voicethread on the parts and vocabulary of the ellipse. At this point, they didn't know any formulas or rules about the ellipse, only the geometry of it. Then today I had them do this all together:

1. (My voice in bold) Draw an ellipse with major axis length 6 and minor axis length 4. 

(After some minor corrections, and with the names changed of course)

Do all of these have the right major and minor axis length? Yes How are they the same, how are they different? All are same shape but oriented differently. If you had had to draw these yesterday, would you all have had the same string length? Yes. And end points? No. Julie and Bridget's ends would be vertical. What would be the same for all endpoints? distance between them. If you had to find their rules, would they all be the same? Horizontal ones will all have same rule and it will be different from the vertical ones.

2. Draw the foci in their approximate locations.

What part of yesterday's lab do the foci represent? ends of string What do you notice about the foci? Lots here: horizontal ones have foci on x axis, vert on y, all hor foci should be in exact same locations and at same distance from each other. Vert ones will be at same dist from each other as the hor but on y axis (based on yesterday that moving the string ends changed the ellipse). Everyone's foci have origin as midpoint. Personality bonus - Julie and Bridget think a bit differently than most - and that's cool.

3. Draw any point on your ellipse in purple.

What from yesterday's lab does your purple point represent? pencil tip What do we call Heather's point? Covertex. Anyone else picked a covertex? Julie. And who picked a vertex? Bridget and Bob. (In both classes, someone picked those key points, fortunately. If they hadn't I would have had to draw my own.)

4. Draw the focal radii for your point.

What do the focal radii represent? the string Who has one focal radius longer than the other? Everybo- no wait. everybody except Julie and Heather. What about Julie and Heather? Theirs are the same length. About how long is Susie's short focal radius....and her long one.....hard to tell huh. But how much must they add up to? 6. Because it's the string, and the major axis is the same length as the string. Who else's d1 + d2 add up to 6? Everyone! Even Julie and Bridget? yup! Why? Bc they have major axis length 6 also, so their strings are 6 units long. So that means how long is Julie's d1? and Heather's d1? 3. 

5. I drew that on Heather's:

What other side length of the green right triangle do we already know? The leg is 2, because it's the semi-minor axis length. So how far from the origin must this focus be? After Pythagoras-ing - it's 2.2. Who else's focus is 2.2 units from the origin? Julie's. Right. How do you know? Because it's the same ellipse just drawn vertically, so it's string ends were the same distance apart. Right. Anyone else whose foci are 2.2 units from the origin? Long pause. OH! Everyone's! Really?!? How do you know that? Not everyone picked a covertex but! Doesn't matter, all foci are at the same distance from centre.

Next we went to Desmos and did this activity to develop the rule. At the end of that, I asked them to type into Desmos x²/9 + y²/4 = 1 and look at the graph. Does it look familiar? Yup we all just drew it. Everyone? Well no, actually, Julie and Bridget didn't. Hm any guesses what we could type in to get their ellipse, which has the same dimensions but is rotated? They got it. x²/4 + y²/9 = 1.

Boom!

Rethinking How We See Mistakes

I had a flashlight moment recently.

I was helping a student to learn how to balance chemical equations. I had done a few examples, and then I had her try one. Part of the procedure calls for a certain amount of trial and error; you try a number in one part of the equation, then you track how it fans out in the rest of the equation. She hesitated for such a long time, that suddenly I realized what was paralyzing her. She thought she was already supposed to know what the right “guess” was. I told her, put any number, fully expect it to be wrong, and then we’ll use it to get the right one. Her response was immediate, she just put down a number, and it was beautifully wrong, because even though I think she had intended it as a “Here you go I told you how stupid I am” moment of self-pity, she immediately said “Oh wait, no, this would be better.” And it was. It wasn’t right, but it was better. Her wrong answer pointed her toward a better one. It seemed like she had needed permission to jump in with a mistake, before she could even experience the unlocking that happened microseconds later.

This has led me to believe that, at least sometimes, we should be calling those “mistakes” something else. Anything that leads to illumination isn’t a “mis”-anything, it’s progress. So from now on, we’re changing our attitude towards mistakes in my class, starting with what we’re calling them - flashlights. If the growth mindset movement is correct, then what we call things affects how we see them and react to them, both on an emotional level and a cognitive one. I think “flashlight” is more positive, and, more importantly, it’s more accurate. Those flashlights are our guides. They show us where the gaps are between what was taught and what was learned. (read more about these gaps in Dylan Wiliam's “Embedded Formative Assessment”.)

Here are a few other ideas I’ve had about changing my own class's attitude toward mistakes.

Praising

When a student makes a mistake, I’m going to praise them at least as much as when they don’t make a mistake. I want them to know that at that moment, they are straight up legit teaching someone something. I’ve been saying “I’m so glad you said that!” or “That’s the best mistake I’ve seen today!” or “I was hoping someone would make that mistake!” That last one I hope makes them feel like they’re my secret accomplices in teaching. It also creates a sort of suspense in my class, like everyone’s waiting for that magic mistake to happen, the same as if it’s a jackpot they’re all trying to hit. Because that’s what it’s going to feel like when they hit it.

Backtracking

We can legitimize mistakes as learning opportunities if we not only talk about what the mistake was, but where it came from. Because mistakes almost always have some truth in them. For example, when kids distribute incorrectly like this: 3(2×4^x) = 3×2×3×4^x, it helps to say to them – I know why you did that, you were thinking 3(2 + 4^x), which would be 3×2 + 3×4^x. I think it’s a relief for them to know that the way they think has some grain of logic to it, at least enough so that another person can backtrack with them to where attention is needed.

Adjectives

If I HAVE to use the word mistake, then I’ll use an adjective like beautiful, glorious, or brilliant before it, because I don’t want mistake to be a bad word – I want it to be a sign that thinking is happening, neurons are firing, lost souls are finding their way. Those are all beautiful and glorious things to happen in class, and I want as many of them as I can get.

Manners

I’ve also been thanking my students for their mistakes, because they're doing some heavy lifting for us all. For example, the other day I asked if log 3 + log 5 could be replaced with a single logarithm using a log property. One student said no, because they didn’t have the same base. Flashlight! She thought the 3 and the 5 were the bases. Not only did this show me that at least one person was looking for the base in the wrong place, but was also not aware that the unwritten base was 10. Two things learned in one shot because of her, so this was a double flashlight, and I thanked her. Later, another student thought that:

 

would lead to xz = y. Flashlight! At least one person was cross multiplying instead of doing fraction multiplication. They learned when that works, and when it doesn’t, and I learned that I am so not ever going to use cross-multiplication ever again. Thanks, kid!

I’m thinking it would be nice if the other kids thanked them too. I’m not sure if I’ll actually get them to, because that would probably be a bit forced. But the way I see it, the kid making a glorious mistake right away in class, as soon as we’ve done something new, is doing everyone a favour. Everyone else can now avoid making it later, when they’re all alone. If that happens, they’ll either not have any idea that they’ve made one, or they won’t have anyone to help them straighten it out. Much better that it happens when we're all there.

Being not perfect

This is a big one, and it’s probably not going to be popular, even with me. I think our kids need us to not just SAY it’s ok to make mistakes, we need to BE okay with them.

Embracing my own mistakes: Because I’m not just talking about their mistakes, I’m talking about mine too. The ones I’m so careful not to ever let them see me doing. That’s why whenever I have to figure something out in front of them I get so totally flustered that I usually say, “Ahem, well kids, I don’t want to take class time to do this, I’ll ahem figure it out later and get back to you. Move along now, nothing to see here.” And I thereby give them the message “Mistakes are great! For you that is, not me. For me they’re embarrassing, humiliating, and scary and they never happen anyway so yeah.” I need to face it, enlist input, and maybe even get help, for example ask “Why do I doubt my answer is right? What kind of answer would make more sense? Up until where did you get the same thing?”

Problem solving on the fly: When a teacher only ever shows students how to solve a problem that they (the teacher) already know how to solve, that’s great, and of course I do that, but we’re really being disingenuous if it stops there. We’re showing them a nice sequence of rules, being fluidly followed by a calm, confident person who is already in possession of the answer, and who therefore couldn’t be any less like them when they’re solving a new problem. I think we need to give our kids the chance to watch how we handle something that is truly new, something in which we truly have no idea what to do first. And show them how we’re not afraid of that feeling, that nobody needs to be afraid of that feeling, because everybody feels that feeling! Let’s get stopped in our tracks together, try stuff together, mess up, go back, sleep on it, admit we're secretly looking for the answer key...you know, normal life.

Reality

But if a mistake happens during a test, it’s very bad, right? We all know what marks do to kids, and how they absolutely halt all learning, whether the marks are good or bad. So yes, of course, I don’t want mistakes happening then, and nobody does. But they will happen, at any time, so I’d rather get the kids armed with strategies to detect and fix them. And most importantly, remain calm.

New Intro to Log Properties

This went well.

I had thought I'd do this via a desmos activity, and I even started to make the slides, but then decided to do it live in class with everyone totally in sync, because I wanted everyone to witness something at the same time.

Here was the sequence, and the narrative, and the results in italics:

No calculators!

What do your order of operations instincts tell you to do first here:  
multiply the 8 and 16

Okay then do it!

Great, and how much is that log?

7

Some discussion here. How did you get that? Some recognized 128 as a power of 2, some did not. I allowed those who weren't as familiar with the powers of 2 to use their calculator ONLY to try out different powers of 2. NO log buttons. I wanted them to COUNT how many 2's were being multiplied, in order to prepare for more counting AND tallying.

Great! How about this one then?  
Some answered 9 very quickly, some answered log base 2 of 512. We discussed both answers. Those who got the 9 quickly were very good at expressing how they did it by using the already-known exponent for 128 and increasing the total number of 2's by the additional 2. My plan worked!

And what about   ?
16. Lit up the board like a Christmas tree. This was what I wanted. Everyone to just count the total number of 2 factors. I pointed out that now they were seeing numbers through a new filter. Now 128 is 2^7, and 512 is 2^9.

Try these the same way - don't actually multiply the arguments, just see them through a filter: 

I'm happy to report that these were very handily answered and justified correctly, by more than just the usual one or two people.

Now comes the real challenge. Let's go back to that first example, and say it in English, along these lines:

After a bit of coaching:

And what's another way of saying "the exponent that 2 needs in order to get 8"?

After just a hint to use the word log......

Let's go back to the other ones you just worked out and say them in English:

This went super fast!

Now let's generalize:

And for the FIRST time in my career, my students told ME the additive property of logs, instead of the other way around. The third line here was supplied, for the first time, by my students:

That felt good.