Tuesday, July 14, 2020

What Happened in My Class After the Shutdown

Mar 13 was the day the Quebec government announced a complete shutdown of Quebec's schools due to the 2020 pandemic. At LEARN's Virtual Campus, that didn't necessarily mean much would change for us, or our students. Theoretically, we could all still attend classes, (as long as there was internet), because we've been used to doing it all online for a long time. The reality was of course that many students stopped attending due to poor connectivity at home, and various other reasons. We did finish our courses, minus any kind of formal assessments, as per our directives, although we did provide our students with practice tests & exams, which were entirely optional.

Our extreme-outlier (until this year that is) situation gave us an immeasurable advantage over all the teachers who were literally thrown into emergency long-distance teaching. We had the luxury of already being thoroughly familiar and comfortable with the online environment, as did our students, so we were able to kind of roll with it by making adjustments for the reduced attendance and reduced expectations. I realize that I was enormously privileged in this regard, and I want to use that privilege in the only way I know - sharing.

No tests and no final June exam meant I had more time during class to do three things:
  • Cover the actual course material better and deeper than I was ever able to previously
  • Cover topics that weren't on the course but were related/cool
  • Do fun stuff just for fun
Today I'll start blogging about it all, starting with a few things I did under the heading...

Covering the course better:

1. Composites and Operations on Functions

When the shutdown happened, we were almost finished the trig function unit. In the past when I've finished this unit I've always wanted to spiral back to operations on functions, and composites of functions, to experiment with them using those beautiful trig curves. Boom. Wish granted. I put together this Desmos activity on Operations on Trig Functions and this one on Composites of Trig Functions, and here are a few shots of what my brilliant students did (anonymizer is on, & for most, original two functions are in blue & green, result in red):

Operations: Students were given 2 trig functions and they
decided which operation to do on them


Operations: Students chose which 2 functions AND which operation

Composites: Students chose which functions to composite, one trig and any other
Lo and behold, gardening and teaching intersected!

At the end of the operations activity, we looked back at a problem that they'd done way back in October, involving multiplication of an exponential function and a trig function. At that time, they didn't know anything about either of those functions. But they did know how to use straight arithmetic to multiply, point by point, two functions (in blue and green) and graph the result (in red):



I remember that back in October, there was great consternation about this question and its solution, even amongst those who understood HOW to do it this way. They were uneasy about it, because this arithmetic method seemed so haphazard, inelegant, and no way to construct the graph of a function - don't we usually use an algebraic rule, which by the way what even would this one be?!? Worry not, I said, all shall be revealed. In previous years, that was a lie, because I never remembered or had time to circle back to it. But this year we had time, and since it was now June, and they were much more sophisticated mathematicians, they now had an opportunity to figure out the rule of the red curve, right on the last slide of the activity. Here is what one student figured out:


The view from my teacher dashboard made me feel like a gardener who'd planted a seed and whose patience has finally paid off with fruit. Next year, I plan to plant a lot more seeds and harvest a lot more fruit! I also think it might be fun to have them work backwards - eg here's the result of a composite, what were the two functions?

2. Function Properties:

This is a topic I'd always circled back to each time we'd added another function to the pile. I already had a Desmos cardsort activity for this, but this year's version had one extra slide at the end. I gave them a bunch of graphs, and asked them to sort them using their own secret headings, which the rest of the class, myself included, would then try to detect:


In order for everyone to see the mystery sortings, I was originally going to share each of their screens myself, from my trusty dashboard, for I am the teacher, and I am so powerful and techy. But since there were so few kids there, I asked them to, one at a time. Each student shared their screen so we could all (myself included) try to guess what criterion they'd used to sort. This turned out to be fun and challenging - I wasn't able to guess some of them. I tweeted about some of them here, but if you're not keen on twitter, here are some screenshots (if you want to see the answers though, they're in the tweet!)

Mystery sort #1


Mystery sort #2


Mystery sort #3


Mystery sort #4
Math and humanity intersected!

I don't know that this activity deepened their math understanding any more than usual, but it stood out to me for other reasons. Getting each student to take turns sharing their screens was powerful. It's so important to establish presence in the online classroom, so that the experience is as human as possible. That goes for students as much as teachers. I'll be getting them to do that a lot more from now on. Also, putting them in the driver's seat, and putting myself in the same boat as them, where I'm as in the dark about the answer as the rest are, models what I'm always saying to them - we're all teachers and we're all learners in this classroom. But as for the math, next time I do this, I'll crank it up a notch by tossing in some additional functions, and getting everyone to sort them according to the current student's scheme. And they won't all be graphs - I'll toss in some other representations while I'm at it. I might as well deepen the math while I'm humanizing!

3. Ellipses:

I gave them this GeoGebra, created by the brilliant Jennifer Silverman (@jensilvermath) so they could draw ellipses and experiment with the impact of changing string length and position of the pins:
I used to just toss my students into this activity without much scaffolding, but this time, because I had fewer students, I structured it a lot better. I gave them all one specific thing to change at a time, say, string length only. I asked one to share their screen, so that the rest watched and discussed what about the ellipse is changing, as well as what isn't changing. The next student to share their screen had a different aspect to vary, eg move one pin only. This made for a much more orderly math discussion, and at the same time was great for creating that group cohesion.

Next I edited Jennifer's to look like this: 


Now everyone had to draw the same ellipse. At this point in the learning cycle, they did not know how to find the locations of the foci, but they did know how long the string had to be (major axis), so the only part they had to trial and error was where to put the pins. But - again, via sharing and discussing, they were able to pin down a few things - pins had to be horizontally oriented, and equidistant from the center C.

All of this I had done in previous years, except as I said for the scaffolding, but this year, thanks to the pandemic, I discovered Classkick, so once they'd learned about the rule of an ellipse, I made this in-class activity:
The original Classkick slides

Sample student work (stickers are part of my feedback)

Sample student work

Classkick was a huge find this year, and if it hadn't been for the pandemic, I might not have known about it. I happened to see a tweet about it from Michael Pershan (@mpershan), who, in his new online classroom situation, wanted to find a way to see his students' work and give feedback quickly. He'd researched many tools and found Classkick.

I have been teaching online for 12 years, I've seen all the things, and this one really turned my head. It's similar to Desmos activities in that from my teacher dashboard, I can watch all my students' writing and actions emerge live, either all students at once or only one of them. But in addition, in Classkick, I can give many different kinds of feedback, including audio (AND STICKERS OMG), and my students can respond to that feedback, either in a chat sidebar, or by writing directly on the screen. Talk about humanizing! It's pretty much like walking around the room as kids work at their desks, except I can see and do so much more than if I were there. There are advantages to this online environment!

Finally, I returned to Jennifer's original GeoGebra, sort of, with this two-part activity, once they knew all the secrets of the ellipse, the geometric ones and the algebraic ones:

Screenshots: 
Part 1: Students draw the ellipse by typing in an algebraic rule

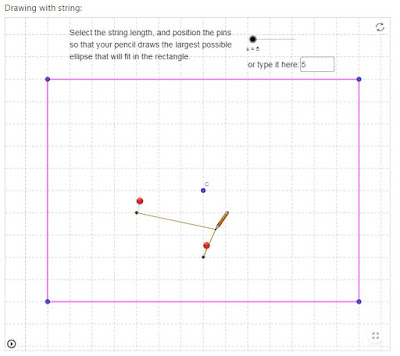Part 2: Students draw the same ellipse by calculating string length and pin positions
All the things happened here. A deeper math dive, group cohesion, gardening, humanity.

Future posts about my pandemic classroom experience shall include:
  • Topics that weren't part of the course but related/cool:

Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)