Recursive Learning Using Geogebra.

Last year was the first year I had my students making geogebra applets. Now that I look back, I think I went too fast at first, because their first function assignment was this. I think it was too much too soon. I may have frightened a few of them....so this year,

I'm slowing down now so I can speed up later.

This time around, they did that same linear function geogebra, but in several layers. I devoted a whole week to letting them get to know geogebra, using the linear function, with which they are already familiar from grade 10. I wanted to start with the linear so that this time around, they're learning about geogebra, as opposed to the math. Although frankly, the two never happen in isolation, but I digress. I had them watch my "Learning Geogebra" video, do the practices that went with them, and then create a new geogebra every day of the week, each one a copy of the previous with more information added to it. I gave feedback on every single version, and helped individuals so that everyone was good before going on to next version. Here's what we did:

Day 1: Create a linear function controlled by sliders for slope and initial value & make sure the graph matches with your own knowledge of the linear function (ie increases for a > 0, flat for a = 0, etc)

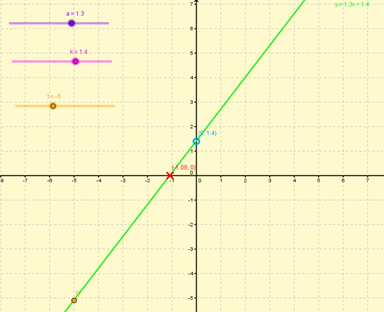
Day 1: Sliders for a and k, rule y = ax + k

Day 2: Add a t-slider and a point P whose position is controlled by the slider, and which slides along the line, no matter how much a and k are. This was really hard for them, partly because they thought that sliders were only for parameters, which was my fault. Will have to do that better next year.

Day 2: t-slider and point P = (t, at + k)

Day 3: Add the initial value and the zero. Developed formula by: Got them to pick their own a and k, calculate I and Z, then use their own ggb to check. Survey everyone's calculations to get pattern, develop formula for I and Z, type in point to geogebra.

Day 3: I = (0, k) and Z = (-k/a, 0)

Day 4: special stuff, like conditional colours depending on whether the function increases or decreases (or is constant), displaying rule/coordinates using the "show value", or by using text boxes with objects in them.

Day 4: Cool fun pretty stuff

Bonus teachable moment

Some students didn't seem familiar with good computing practices such as saving subsequent versions with a new name, or file naming practices. The version created on day 1 was linear1, day 2 was linear2, etc. I discovered this when one student sighed and said it was tiring having to start all over each time....

And on that note, I made this for them:

And now, for the rest of this year, they're going to make geogebras AND USE THEM!!! To make more!!!!

I want them to do this for EVERY function we're studying. And not only make geogebras, but USE them. And not just because I tell them to, but because they are compelled to, in order to move their own learning forward, in whatever direction they choose. I'm seeing a cyclical formation, in which they use their own paper graphs, their own calculations, and their own instincts to create, use, then improve their geogebras, which then feed the next one...

The recursive learning: Create - Check - Use - Repeat

This week we're starting the absolute value function. Here's what I'm planning:

Tuesday: (Yesterday) Graph, on graph paper, many graphs of absolute value functions, and worked their way up until they could quickly graph and describe y = a |b(x - h)| + k. So now they knew what a graph should look like and why it looks that way.
Wednesday: (Today) Create version 1 with sliders for a, b, h, and k, and verify they're doing what they should by comparing to paper graphs. Also put in a vertex with (h, k) and make sure it's where it should be.

Thursday: Math lab! Use version 1 to explore relationships between parameters, to develop point P.
Friday: Create version 2 with time slider and point P, verify it using own calculations
Next week: To add initial value, domain, range, interval of increase etc

New Rule: Trust yourself first, geogebra second

What I really, really want to EMPHASIZE is that they verify, as much as possible, their own geogebra, using their own calculations, and not vice versa. Most importantly they verify NOT by showing it to ME and asking ME if it's right.

If this works, by the time they're done this, they will know the absolute value function like a boss!

And by the end of the year, they'll be total geogebrainiacs like me!